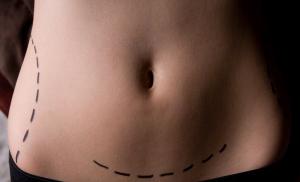
Distance between point and line. The simplest problems with a straight line on a plane

This article talks about the topic « distance from point to line », the determination of the distance from a point to a straight line with illustrated examples by the method of coordinates is considered. Each block of the theory at the end has shown examples of solving similar problems.

Yandex.RTB R-A-339285-1

The distance from a point to a straight line is found through the definition of the distance from a point to a point. Let's take a closer look.

Let there be a straight line a and a point M 1 that does not belong to a given straight line. Draw line b through it, which is perpendicular to line a. The point of intersection of the lines is taken as H 1. We get that M 1 H 1 is the perpendicular, which was lowered from the point M 1 to the line a.

Definition 1

Distance from point М 1 to line a called the distance between points M 1 and H 1.

There are definition records with the figure of the length of the perpendicular.

Definition 2

Distance from point to line is the length of the perpendicular drawn from a given point to a given straight line.

The definitions are equivalent. Consider the figure below.

It is known that the distance from a point to a straight line is the smallest of all possible. Let's look at an example.

If we take a point Q lying on the line a, not coinciding with the point M 1, then we get that the segment M 1 Q is called inclined, dropped from M 1 to the line a. It is necessary to designate that the perpendicular from the point M 1 is less than any other inclined line drawn from the point to the straight line.

To prove this, consider a triangle M 1 Q 1 H 1, where M 1 Q 1 is the hypotenuse. It is known that its length is always greater than the length of any of the legs. We have that M 1 H 1< M 1 Q . Рассмотрим рисунок, приведенный ниже.

The initial data for finding from a point to a straight line allows you to use several solution methods: through the Pythagorean theorem, determining the sine, cosine, tangent of an angle, and others. Most tasks of this type are solved at school in geometry lessons.

When, when finding the distance from a point to a straight line, it is possible to enter a rectangular coordinate system, then the coordinate method is used. In this paragraph, we will consider the main two methods for finding the desired distance from a given point.

The first method involves finding the distance as a perpendicular drawn from M 1 to the straight line a. The second method uses the normal equation of the straight line a to find the desired distance.

If there is a point on the plane with coordinates M 1 (x 1, y 1), located in a rectangular coordinate system, straight line a, and you need to find the distance M 1 H 1, you can calculate in two ways. Let's consider them.

The first way

If there are coordinates of the point H 1 equal to x 2, y 2, then the distance from the point to the straight line is calculated by the coordinates from the formula M 1 H 1 = (x 2 - x 1) 2 + (y 2 - y 1) 2.

Now let's move on to finding the coordinates of the point H 1.

It is known that a straight line in O x y corresponds to the equation of a straight line on a plane. Let's take a way of specifying a straight line a through writing the general equation of a straight line or an equation with a slope. We compose the equation of the straight line that passes through the point M 1 perpendicular to the given straight line a. The straight line will be denoted by beech b. H 1 is the point of intersection of lines a and b, which means that to determine the coordinates, you must use the article, which deals with the coordinates of the points of intersection of two lines.

It can be seen that the algorithm for finding the distance from a given point M 1 (x 1, y 1) to a straight line a is carried out according to points:

Definition 3

• finding the general equation of the straight line a, having the form A 1 x + B 1 y + C 1 = 0, or an equation with a slope, having the form y = k 1 x + b 1;
• obtaining a general equation of line b, having the form A 2 x + B 2 y + C 2 = 0 or an equation with a slope y = k 2 x + b 2, if line b intersects point M 1 and is perpendicular to a given line a;
• determination of the coordinates x 2, y 2 of the point H 1, which is the intersection point of a and b, for this, a system of linear equations is solved A 1 x + B 1 y + C 1 = 0 A 2 x + B 2 y + C 2 = 0 or y = k 1 x + b 1 y = k 2 x + b 2;
• calculating the required distance from a point to a straight line using the formula M 1 H 1 = (x 2 - x 1) 2 + (y 2 - y 1) 2.

Second way

The theorem can help answer the question of finding the distance from a given point to a given straight line on a plane.

Theorem

The rectangular coordinate system has O x y has a point M 1 (x 1, y 1), from which a straight line a is drawn to the plane, given by the normal equation of the plane, which has the form cos α x + cos β y - p = 0, is equal to to the modulus of the value obtained on the left-hand side of the normal equation of the straight line, calculated at x = x 1, y = y 1, which means that M 1 H 1 = cos α x 1 + cos β y 1 - p.

Proof

Line a corresponds to the normal equation of the plane, which has the form cos α x + cos β y - p = 0, then n → = (cos α, cos β) is considered the normal vector of the line a at a distance from the origin to the line a with p units ... It is necessary to display all the data in the figure, add a point with coordinates M 1 (x 1, y 1), where the radius vector of the point M 1 - O M 1 → = (x 1, y 1). It is necessary to draw a straight line from a point to a straight line, which we denote by M 1 H 1. It is necessary to show the projections M 2 and H 2 of points M 1 and H 2 onto a straight line passing through point O with a direction vector of the form n → = (cos α, cos β), and the numerical projection of the vector is denoted as OM 1 → = (x 1, y 1) to the direction n → = (cos α, cos β) as npn → OM 1 →.

Variations depend on the location of the point M 1 itself. Consider in the figure below.

We fix the results using the formula M 1 H 1 = n p n → O M → 1 - p. Then we reduce the equality to this form M 1 H 1 = cos α x 1 + cos β y 1 - p in order to obtain n p n → O M → 1 = cos α x 1 + cos β y 1.

The scalar product of vectors as a result gives a transformed formula of the form n →, OM → 1 = n → npn → OM 1 → = 1 npn → OM 1 → = npn → OM 1 →, which is a product in coordinate form of the form n →, OM 1 → = cos α x 1 + cos β y 1. Hence, we obtain that n p n → O M 1 → = cos α x 1 + cos β y 1. It follows that M 1 H 1 = n p n → O M 1 → - p = cos α x 1 + cos β y 1 - p. The theorem is proved.

We get that to find the distance from the point M 1 (x 1, y 1) to the straight line a on the plane, you need to perform several actions:

Definition 4

• obtaining the normal equation of the straight line a cos α x + cos β y - p = 0, provided that it is not in the task;
• calculation of the expression cos α · x 1 + cos β · y 1 - p, where the obtained value takes M 1 H 1.

Let us apply these methods to solving problems with finding the distance from a point to a plane.

Example 1

Find the distance from the point with coordinates M 1 (- 1, 2) to the straight line 4 x - 3 y + 35 = 0.

Solution

Let's apply the first method to solve.

To do this, it is necessary to find the general equation of the straight line b, which passes through a given point M 1 (- 1, 2), perpendicular to the straight line 4 x - 3 y + 35 = 0. It is seen from the condition that the line b is perpendicular to the line a, then its direction vector has coordinates equal to (4, - 3). Thus, we have the opportunity to write the canonical equation of the straight line b on the plane, since there are coordinates of the point M 1, belongs to the straight line b. Determine the coordinates of the direction vector of the straight line b. We get x - (- 1) 4 = y - 2 - 3 ⇔ x + 1 4 = y - 2 - 3. The resulting canonical equation must be transformed to the general one. Then we get that

x + 1 4 = y - 2 - 3 ⇔ - 3 (x + 1) = 4 (y - 2) ⇔ 3 x + 4 y - 5 = 0

Let us find the coordinates of the points of intersection of straight lines, which we will take as the designation H 1. The transformations look like this:

4 x - 3 y + 35 = 0 3 x + 4 y - 5 = 0 ⇔ x = 3 4 y - 35 4 3 x + 4 y - 5 = 0 ⇔ x = 3 4 y - 35 4 3 3 4 y - 35 4 + 4 y - 5 = 0 ⇔ ⇔ x = 3 4 y - 35 4 y = 5 ⇔ x = 3 4 5 - 35 4 y = 5 ⇔ x = - 5 y = 5

From the above, we have that the coordinates of the point H 1 are (- 5; 5).

It is necessary to calculate the distance from point M 1 to line a. We have that the coordinates of the points M 1 (- 1, 2) and H 1 (- 5, 5), then we substitute in the formula for finding the distance and we get that

M 1 H 1 = (- 5 - (- 1) 2 + (5 - 2) 2 = 25 = 5

Second solution.

In order to solve in another way, it is necessary to obtain the normal equation of the straight line. Evaluate the normalizing factor and multiply both sides of the equation 4 x - 3 y + 35 = 0. From this we get that the normalizing factor is - 1 4 2 + (- 3) 2 = - 1 5, and the normal equation will be of the form - 1 5 4 x - 3 y + 35 = - 1 5 0 ⇔ - 4 5 x + 3 5 y - 7 = 0.

According to the calculation algorithm, it is necessary to obtain the normal equation of the straight line and calculate it with the values ​​x = - 1, y = 2. Then we get that

4 5 - 1 + 3 5 2 - 7 = - 5

Hence, we obtain that the distance from the point M 1 (- 1, 2) to the given straight line 4 x - 3 y + 35 = 0 has the value - 5 = 5.

Answer: 5 .

It can be seen that in this method it is important to use the normal equation of a straight line, since this method is the shortest. But the first method is convenient in that it is consistent and logical, although it has more calculation points.

Example 2

On the plane there is a rectangular coordinate system O x y with a point M 1 (8, 0) and a straight line y = 1 2 x + 1. Find the distance from a given point to a straight line.

Solution

The solution in the first way implies the reduction of the given equation with the slope to the general equation. For simplicity, you can do it differently.

If the product of the slopes of the perpendicular lines has a value of - 1, then the slope of the line perpendicular to the given y = 1 2 x + 1 has the value 2. Now we get the equation of the straight line passing through the point with coordinates M 1 (8, 0). We have that y - 0 = - 2 (x - 8) ⇔ y = - 2 x + 16.

We turn to finding the coordinates of the point H 1, that is, the intersection points y = - 2 x + 16 and y = 1 2 x + 1. We compose a system of equations and get:

y = 1 2 x + 1 y = - 2 x + 16 ⇔ y = 1 2 x + 1 1 2 x + 1 = - 2 x + 16 ⇔ y = 1 2 x + 1 x = 6 ⇔ ⇔ y = 1 2 6 + 1 x = 6 = y = 4 x = 6 ⇒ H 1 (6, 4)

It follows that the distance from the point with coordinates M 1 (8, 0) to the straight line y = 1 2 x + 1 is equal to the distance from the start point and the end point with coordinates M 1 (8, 0) and H 1 (6, 4) ... Let's calculate and get that M 1 H 1 = 6 - 8 2 + (4 - 0) 2 20 = 2 5.

The solution in the second way is to go from an equation with a coefficient to its normal form. That is, we get y = 1 2 x + 1 ⇔ 1 2 x - y + 1 = 0, then the value of the normalizing factor will be - 1 1 2 2 + (- 1) 2 = - 2 5. It follows that the normal equation of the line takes the form - 2 5 1 2 x - y + 1 = - 2 5 0 ⇔ - 1 5 x + 2 5 y - 2 5 = 0. Let's make a calculation from the point M 1 8, 0 to a straight line of the form - 1 5 x + 2 5 y - 2 5 = 0. We get:

M 1 H 1 = - 1 5 8 + 2 5 0 - 2 5 = - 10 5 = 2 5

Answer: 2 5 .

Example 3

It is necessary to calculate the distance from the point with coordinates M 1 (- 2, 4) to the straight lines 2 x - 3 = 0 and y + 1 = 0.

Solution

We obtain the equation of the normal form of the straight line 2 x - 3 = 0:

2 x - 3 = 0 ⇔ 1 2 2 x - 3 = 1 2 0 ⇔ x - 3 2 = 0

Then we proceed to calculating the distance from the point M 1 - 2, 4 to the straight line x - 3 2 = 0. We get:

M 1 H 1 = - 2 - 3 2 = 3 1 2

The equation of the straight line y + 1 = 0 has a normalizing factor of -1. This means that the equation will take the form - y - 1 = 0. We proceed to calculating the distance from the point M 1 (- 2, 4) to the straight line - y - 1 = 0. We get that it is equal to - 4 - 1 = 5.

Answer: 3 1 2 and 5.

Let us consider in detail the finding of the distance from a given point of the plane to the coordinate axes O x and O y.

In a rectangular coordinate system, the O y axis has an equation of a straight line, which is incomplete, has the form x = 0, and O x - y = 0. The equations are normal for the coordinate axes, then you need to find the distance from the point with coordinates M 1 x 1, y 1 to straight lines. This is done based on the formulas M 1 H 1 = x 1 and M 1 H 1 = y 1. Consider in the figure below.

Example 4

Find the distance from the point M 1 (6, - 7) to the coordinate lines located in the plane O x y.

Solution

Since the equation y = 0 refers to the straight line O x, you can find the distance from M 1 with the given coordinates to this straight line using the formula. We get that 6 = 6.

Since the equation x = 0 refers to the straight line O y, you can find the distance from M 1 to this straight line using the formula. Then we get that - 7 = 7.

Answer: the distance from M 1 to O x has a value of 6, and from M 1 to O y has a value of 7.

When in three-dimensional space we have a point with coordinates M 1 (x 1, y 1, z 1), it is necessary to find the distance from point A to line a.

Consider two ways that allow you to calculate the distance from a point to a straight line a located in space. The first case considers the distance from the point M 1 to the straight line, where the point on the straight line is called H 1 and is the base of the perpendicular drawn from the point M 1 to the straight line a. The second case suggests that the points of this plane must be sought as the height of the parallelogram.

The first way

From the definition, we have that the distance from the point M 1, located on the straight line a, is the length of the perpendicular M 1 H 1, then we get that with the found coordinates of the point H 1, then we find the distance between M 1 (x 1, y 1, z 1 ) and H 1 (x 1, y 1, z 1), based on the formula M 1 H 1 = x 2 - x 1 2 + y 2 - y 1 2 + z 2 - z 1 2.

We get that the whole solution goes to find the coordinates of the base of the perpendicular drawn from М 1 to the line a. This is done as follows: H 1 is the point where the straight line a intersects with the plane that passes through the given point.

Hence, the algorithm for determining the distance from the point M 1 (x 1, y 1, z 1) to the line a in space implies several points:

Definition 5

• drawing up the equation of the χ plane as the equation of the plane passing through a given point that is perpendicular to the straight line;
• determination of coordinates (x 2, y 2, z 2) belonging to the point H 1, which is the point of intersection of the straight line a and the plane χ;
• calculating the distance from a point to a straight line using the formula M 1 H 1 = x 2 - x 1 2 + y 2 - y 1 2 + z 2 - z 1 2.

Second way

From the condition we have a straight line a, then we can determine the direction vector a → = a x, a y, a z with coordinates x 3, y 3, z 3 and a certain point M 3 belonging to the straight line a. If there are coordinates of points M 1 (x 1, y 1) and M 3 x 3, y 3, z 3, you can calculate M 3 M 1 →:

M 3 M 1 → = (x 1 - x 3, y 1 - y 3, z 1 - z 3)

It is necessary to postpone the vectors a → = a x, a y, a z and M 3 M 1 → = x 1 - x 3, y 1 - y 3, z 1 - z 3 from the point M 3, connect and get a parallelogram figure. M 1 H 1 is the height of the parallelogram.

Consider in the figure below.

We have that the height M 1 H 1 is the desired distance, then it is necessary to find it by the formula. That is, we are looking for M 1 H 1.

We denote the area of ​​the parallelogram for the letter S, is found by the formula using the vector a → = (a x, a y, a z) and M 3 M 1 → = x 1 - x 3. y 1 - y 3, z 1 - z 3. The area formula is S = a → × M 3 M 1 →. Also, the area of ​​the figure is equal to the product of the lengths of its sides by the height, we get that S = a → M 1 H 1 with a → = ax 2 + ay 2 + az 2, which is the length of the vector a → = (ax, ay, az), which is equal to the side of the parallelogram. Hence, M 1 H 1 is the distance from a point to a line. It is found by the formula M 1 H 1 = a → × M 3 M 1 → a →.

To find the distance from a point with coordinates M 1 (x 1, y 1, z 1) to a straight line a in space, it is necessary to perform several steps of the algorithm:

Definition 6

• determination of the directing vector of the straight line a - a → = (a x, a y, a z);
• calculating the length of the direction vector a → = a x 2 + a y 2 + a z 2;
• obtaining coordinates x 3, y 3, z 3 belonging to the point M 3 located on the straight line a;
• calculation of the coordinates of the vector M 3 M 1 →;
• finding the vector product of vectors a → (ax, ay, az) and M 3 M 1 → = x 1 - x 3, y 1 - y 3, z 1 - z 3 as a → × M 3 M 1 → = i → j → k → axayazx 1 - x 3 y 1 - y 3 z 1 - z 3 to obtain the length by the formula a → × M 3 M 1 →;
• calculating the distance from a point to a straight line M 1 H 1 = a → × M 3 M 1 → a →.

Solving problems on finding the distance from a given point to a given straight line in space

Example 5

Find the distance from the point with coordinates M 1 2, - 4, - 1 to the line x + 1 2 = y - 1 = z + 5 5.

Solution

The first method begins with writing the equation of the χ plane passing through M 1 and perpendicular to a given point. We get an expression of the form:

2 (x - 2) - 1 (y - (- 4)) + 5 (z - (- 1)) = 0 ⇔ 2 x - y + 5 z - 3 = 0

It is necessary to find the coordinates of the point H 1, which is the point of intersection with the plane χ to the line specified by the condition. You should go from canonical to intersecting. Then we get a system of equations of the form:

x + 1 2 = y - 1 = z + 5 5 ⇔ - 1 (x + 1) = 2 y 5 (x + 1) = 2 (z + 5) 5 y = - 1 (z + 5) ⇔ x + 2 y + 1 = 0 5 x - 2 z - 5 = 0 5 y + z + 5 = 0 ⇔ x + 2 y + 1 = 0 5 x - 2 z - 5 = 0

It is necessary to calculate the system x + 2 y + 1 = 0 5 x - 2 z - 5 = 0 2 x - y + 5 z - 3 = 0 ⇔ x + 2 y = - 1 5 x - 2 z = 5 2 x - y + 5 z = 3 according to Cramer's method, then we get that:

∆ = 1 2 0 5 0 - 2 2 - 1 5 = - 60 ∆ x = - 1 2 0 5 0 - 2 3 - 1 5 = - 60 ⇔ x = ∆ x ∆ = - 60 - 60 = 1 ∆ y = 1 - 1 0 5 5 2 2 3 5 = 60 ⇒ y = ∆ y ∆ = 60 - 60 = - 1 ∆ z = 1 2 - 1 5 0 5 2 - 1 3 = 0 ⇒ z = ∆ z ∆ = 0 - 60 = 0

Hence we have that H 1 (1, - 1, 0).

M 1 H 1 = 1 - 2 2 + - 1 - - 4 2 + 0 - - 1 2 = 11

The second way is to start by looking for coordinates in the canonical equation. To do this, you need to pay attention to the denominators of the fraction. Then a → = 2, - 1, 5 is the direction vector of the line x + 1 2 = y - 1 = z + 5 5. It is necessary to calculate the length by the formula a → = 2 2 + (- 1) 2 + 5 2 = 30.

It is clear that the line x + 1 2 = y - 1 = z + 5 5 intersects the point M 3 (- 1, 0, - 5), hence we have that the vector with the origin M 3 (- 1, 0, - 5) and its end at point M 1 2, - 4, - 1 is M 3 M 1 → = 3, - 4, 4. Find the vector product a → = (2, - 1, 5) and M 3 M 1 → = (3, - 4, 4).

We get an expression of the form a → × M 3 M 1 → = i → j → k → 2 - 1 5 3 - 4 4 = - 4 i → + 15 j → - 8 k → + 20 i → - 8 J → = 16 i → + 7 j → - 5 k →

we get that the length of the vector product is a → × M 3 M 1 → = 16 2 + 7 2 + - 5 2 = 330.

We have all the data for using the formula for calculating the distance from a point for a straight line, so we apply it and get:

M 1 H 1 = a → × M 3 M 1 → a → = 330 30 = 11

Answer: 11 .

If you notice an error in the text, please select it and press Ctrl + Enter

The distance from a point to a straight line is the length of the perpendicular dropped from a point to a straight line. In descriptive geometry, it is determined graphically using the algorithm below.

Algorithm

1. The straight line is transferred to a position in which it will be parallel to any projection plane. For this, methods of transforming orthogonal projections are used.
2. From a point, a perpendicular is drawn to a straight line. This construction is based on the right angle projection theorem.
3. The length of a perpendicular is determined by transforming its projections or using the right triangle method.

The following figure shows a complex drawing of point M and line b defined by segment CD. It is required to find the distance between them.

According to our algorithm, the first thing to do is to move the line to a position parallel to the projection plane. It is important to understand that after the transformations, the actual distance between the point and the line should not change. That is why it is convenient to use the method of replacing planes here, which does not imply the movement of figures in space.

The results of the first stage of construction are shown below. The figure shows how an additional frontal plane P 4 is introduced parallel to b. In the new system (P 1, P 4) points C "" 1, D "" 1, M "" 1 are at the same distance from the X axis 1 as C "", D "", M "" from the axis X.

Performing the second part of the algorithm, from M "" 1 we lower the perpendicular M "" 1 N "" 1 to the straight line b "" 1, since the right angle MND between b and MN is projected onto the plane P 4 in full size. On the communication line, determine the position of the point N "and carry out the projection M" N "of the segment MN.

At the final stage, you need to determine the value of the segment MN by its projections M "N" and M "" 1 N "" 1. To do this, we build a right-angled triangle M "" 1 N "" 1 N 0, whose leg N "" 1 N 0 is equal to the difference (Y M 1 - Y N 1) of the distance of points M "and N" from the X 1 axis. The length of the hypotenuse M "" 1 N 0 of the triangle M "" 1 N "" 1 N 0 corresponds to the desired distance from M to b.

Second solution

• Parallel to CD, we introduce a new frontal plane P 4. It intersects П 1 along the X 1 axis, and X 1 ∥C "D". In accordance with the method of replacing planes, we determine the projections of points C "" 1, D "" 1 and M "" 1, as shown in the figure.
• Perpendicular to C "" 1 D "" 1 we build an additional horizontal plane P 5, onto which the straight line b is projected to the point C "2 = b" 2.
• The distance between point M and line b is determined by the length of the segment M "2 C" 2, marked in red.

Similar tasks:

First level

Coordinates and vectors. Comprehensive guide (2019)

In this article, we will begin a discussion of one "magic wand" that will allow you to reduce many geometry problems to simple arithmetic. This "stick" can make your life much easier, especially in the case when you feel insecure in the construction of spatial figures, sections, etc. All this requires a certain imagination and practical skills. The method, which we will begin to consider here, will allow you to abstract almost completely from all kinds of geometric constructions and reasoning. The method is called "Coordinate method"... In this article, we will consider the following questions:

1. Coordinate plane
2. Points and vectors on the plane
3. Constructing a vector from two points
4. Vector length (distance between two points)
5. Midpoint coordinates
6. Dot product of vectors
7. Angle between two vectors

I think you already guessed why the coordinate method is called that? It is true that he received such a name, since he operates not with geometric objects, but with their numerical characteristics (coordinates). And the transformation itself, which makes it possible to go from geometry to algebra, consists in introducing a coordinate system. If the original figure was flat, then the coordinates are two-dimensional, and if the figure is three-dimensional, then the coordinates are three-dimensional. In this article, we will only consider the two-dimensional case. And the main goal of the article is to teach you how to use some basic techniques of the coordinate method (they sometimes turn out to be useful in solving problems on planimetry in part B of the exam). The next two sections on this topic are devoted to the discussion of methods for solving problems C2 (the problem of stereometry).

Where would it be logical to start discussing the coordinate method? Probably from the concept of a coordinate system. Remember when you first encountered her. It seems to me that in the 7th grade, when you learned about the existence of a linear function, for example. Let me remind you that you built it point by point. Do you remember? You chose an arbitrary number, substituted it into the formula and calculated that way. For example, if, then, if, then, etc. What did you get in the end? And you received points with coordinates: and. Then you drew a "cross" (coordinate system), chose a scale on it (how many cells you will have as a unit segment) and marked on it the points you received, which you then connected with a straight line, the resulting line is the graph of the function.

There are several points here that should be explained to you in a little more detail:

1. You choose a single segment for reasons of convenience, so that everything fits nicely and compactly in the picture.

2. It is assumed that the axis goes from left to right, and the axis goes from bottom to top.

3. They intersect at right angles, and the point of their intersection is called the origin. It is indicated by a letter.

4. In writing the coordinates of a point, for example, on the left in brackets is the coordinate of the point along the axis, and on the right, along the axis. In particular, it simply means that at the point

5. In order to set any point on the coordinate axis, you need to specify its coordinates (2 numbers)

6. For any point on the axis,

7. For any point on the axis,

8. The axis is called the abscissa axis.

9. The axis is called the y-axis.

Now let's take the next step with you: mark two points. Let's connect these two points with a segment. And we will put the arrow as if we were drawing a segment from point to point: that is, we will make our segment directed!

Remember, what else is a directional line called? That's right, it's called a vector!

Thus, if we connect a point with a point, moreover, the beginning will be point A, and the end will be point B, then we get a vector. You also did this formation in the 8th grade, remember?

It turns out that vectors, like points, can be denoted by two numbers: these numbers are called the coordinates of the vector. The question is: do you think it is enough for us to know the coordinates of the beginning and end of the vector to find its coordinates? It turns out that yes! And this is done very simply:

Thus, since the point in the vector is the beginning and a is the end, the vector has the following coordinates:

For example, if, then the coordinates of the vector

Now let's do the opposite, find the coordinates of the vector. What do we need to change for this? Yes, you need to swap the beginning and the end: now the beginning of the vector will be at the point, and the end will be at the point. Then:

Look closely, how are vectors and? Their only difference is the signs in the coordinates. They are opposite. It is customary to write this fact like this:

Sometimes, if it is not specifically specified which point is the beginning of the vector, and which is the end, then vectors are denoted not by two capital letters, but by one lowercase, for example:, etc.

Now a little practice yourself and find the coordinates of the following vectors:

Examination:

Now solve the problem a little harder:

Vektor with na-cha-lom at the point has co-or-di-na-ty. Nay-di-those abs-cis-su points.

All the same is rather prosaic: Let be the coordinates of a point. Then

I made up the system by definition of what the coordinates of a vector are. Then the point has coordinates. We are interested in the abscissa. Then

Answer:

What else can you do with vectors? Yes, almost everything is the same as with ordinary numbers (except that you cannot divide, but you can multiply in two ways, one of which we will discuss here a little later)

1. Vectors can be added to each other
2. Vectors can be subtracted from each other
3. Vectors can be multiplied (or divided) by an arbitrary nonzero number
4. Vectors can be multiplied by each other

All these operations have a very clear geometric representation. For example, the triangle (or parallelogram) rule for addition and subtraction:

The vector expands or contracts or changes direction when multiplied or divided by a number:

However, here we will be interested in the question of what is happening with the coordinates.

1. When adding (subtracting) two vectors, we add (subtract) their coordinates element by element. That is:

2. When multiplying (dividing) a vector by a number, all its coordinates are multiplied (divided) by this number:

For example:

· Nay-di-te sum of ko-or-di-nat vek-to-ra.

Let's first find the coordinates of each of the vectors. They both have the same origin - the origin point. Their ends are different. Then, . Now let's calculate the coordinates of the vector Then the sum of the coordinates of the resulting vector is.

Answer:

Now solve the following problem yourself:

Find the sum of the coordinates of a vector

We check:

Let's now consider the following problem: we have two points on the coordinate plane. How to find the distance between them? Let the first point be, and the second. Let's denote the distance between them through. Let's make the following drawing for clarity:

What I've done? I, firstly, connected the points and, and also from the point I drew a line parallel to the axis, and from the point I drew a line parallel to the axis. Did they intersect at a point, thus forming a wonderful figure? What is it remarkable for? Yes, you and I know almost everything about a right-angled triangle. Well, the Pythagorean theorem - for sure. The sought segment is the hypotenuse of this triangle, and the segments are the legs. What are the coordinates of a point? Yes, they are easy to find from the picture: Since the segments are parallel to the axes and, accordingly, their lengths are easy to find: if you denote the lengths of the segments, respectively, by, then

Now let's use the Pythagorean theorem. We know the lengths of the legs, we will find the hypotenuse:

Thus, the distance between two points is the root of the sum of the squares of the differences from the coordinates. Or - the distance between two points is the length of the line that connects them. It is easy to see that the distance between points is independent of direction. Then:

From this we draw three conclusions:

Let's do a little practice calculating the distance between two points:

For example, if, then the distance between and is equal to

Or let's go differently: find the coordinates of the vector

And find the length of the vector:

As you can see, the same thing!

Now do some practice yourself:

Task: find the distance between the specified points:

We check:

Here are a couple more problems for the same formula, although they sound a little different:

1. Nay-di-te square-rat of the length of the century-to-ra.

2. Nay-di-te square-rat of the length of the century-to-ra

I think you did it easily with them? We check:

1. And this is for attention) We have already found the coordinates of the vectors and earlier:. Then the vector has coordinates. The square of its length will be equal to:

2. Find the coordinates of the vector

Then the square of its length is

Nothing complicated, right? Simple arithmetic, nothing more.

The following tasks cannot be categorized unambiguously, they are more likely to general erudition and the ability to draw simple pictures.

1. Nay-di-te sine of an angle on-to-on from-cut, co-uni-nya-yu-shch-th point, with the abscissa axis.

and

What are we going to do here? You need to find the sine of the angle between and the axis. And where do we know how to look for a sine? That's right, in a right-angled triangle. So what do we need to do? Build this triangle!

Since the coordinates of the point are and, the segment is equal, and the segment. We need to find the sine of the angle. Let me remind you that the sinus is the ratio of the opposite leg to the hypotenuse, then

What is left for us to do? Find the hypotenuse. You can do it in two ways: by the Pythagorean theorem (the legs are known!) Or by the formula for the distance between two points (in fact, the same thing as the first way!). I will go the second way:

Answer:

The next task will seem even easier to you. She - on the coordinates of the point.

Objective 2. Per-pen-di-ku-lar is lowered from the point to the abs-ciss axis. Nay-di-te abs-cis-su os-no-va-nia per-pen-di-ku-la-ra.

Let's make a drawing:

The base of the perpendicular is the point at which it crosses the abscissa axis (axis), for me this is the point. The figure shows that it has coordinates:. We are interested in the abscissa - that is, the "x" component. It is equal.

Answer: .

Objective 3. Under the conditions of the previous problem, find the sum of the distances from a point to the coordinate axes.

The task is generally elementary, if you know what the distance from a point to the axes is. You know? I hope, but I still remind you:

So, in my picture, located a little higher, I have already drawn one such perpendicular? Which axis is it to? To the axis. And then what is its length equal to? It is equal. Now draw the perpendicular to the axis yourself and find its length. It will be equal, right? Then their sum is equal.

Answer: .

Task 4. In the conditions of problem 2, find the ordinate of the point symmetrical to the point relative to the abscissa axis.

I think you intuitively understand what symmetry is? Many objects have it: many buildings, tables, airplanes, many geometric shapes: a ball, cylinder, square, rhombus, etc. Roughly speaking, symmetry can be understood as follows: a figure consists of two (or more) identical halves. This symmetry is called axial. What then is an axis? This is exactly the line along which a figure can, relatively speaking, be "cut" into identical halves (in this picture, the axis of symmetry is a straight line):

Now let's get back to our problem. We know that we are looking for a point that is symmetrical about the axis. Then this axis is the axis of symmetry. This means that we need to mark a point so that the axis cuts the segment into two equal parts. Try to mark such a point yourself. Now compare with my solution:

Did you do the same? OK! At the found point, we are interested in the ordinate. She is equal

Answer:

Now tell me, after thinking about seconds, what will be the abscissa of the point symmetrical to point A relative to the ordinate? What is your answer? Correct answer: .

In general, the rule can be written like this:

A point symmetrical to a point relative to the abscissa axis has coordinates:

A point symmetrical to a point about the ordinate axis has coordinates:

Well, now it's completely scary task: find the coordinates of the point symmetrical to the point, relative to the origin. You first think for yourself, and then look at my drawing!

Answer:

Now parallelogram problem:

Problem 5: The points are ver-shi-na-mi paral-le-lo-gram-ma. Nay-di-te or-di-na-tu points.

You can solve this problem in two ways: logic and the method of coordinates. I will first apply the coordinate method, and then I will tell you how you can solve it differently.

It is quite clear that the abscissa of the point is equal to. (it lies on the perpendicular drawn from a point to the abscissa axis). We need to find the ordinate. Let's take advantage of the fact that our figure is a parallelogram, which means that. Find the length of the segment using the formula for the distance between two points:

We lower the perpendicular connecting the point to the axis. The intersection point will be marked with a letter.

The segment length is. (find the problem itself, where we discussed this point), then we find the length of the segment by the Pythagorean theorem:

The length of the line is exactly the same as its ordinate.

Answer: .

Another solution (I'll just give a picture that illustrates it)

Solution progress:

1. Conduct

2. Find the coordinates of the point and the length

3. Prove that.

Another one segment length puzzle:

The points appear-la-are-Xia ver-shi-na-mi tre-coal-ni-ka. Nay-di-te is the length of its middle line, paral-lel-noy.

Do you remember what the middle line of a triangle is? Then this task is elementary for you. If you don’t remember, then I will remind you: the middle line of a triangle is the line that connects the midpoints of opposite sides. It is parallel to the base and equal to half of it.

The base is a line segment. We had to look for its length earlier, it is equal. Then the length of the middle line is half and equal.

Answer: .

Commentary: this problem can be solved in another way, which we will turn to a little later.

In the meantime - here are a few tasks for you, practice them, they are quite simple, but they help you to "get your hand" using the method of coordinates!

1. The points are the ver-shi-na-mi tra-petsii. Nay-di-te is the length of its middle line.

2. Dots and are-la-sy-ver-shi-na-mi pa-ra-le-lo-gram-ma. Nay-di-te or-di-na-tu points.

3. Nay-di-te length from-cut, co-single-nya-yu-shch-go point and

4. Nay-di-te area of ​​the beautiful fi-gu-ry on the co-or-di-nat-noy plane.

5. The circle with the center at na-cha-le ko-or-di-nat passes through the point. Nay-di-te her ra-di-us.

6. Nai-di-te ra-di-us of the circle, described-san-noy near the rectangular-nik-ka, the vertices of ko-to-ro-go have a co-op -di-na-you co-vet-but

Solutions:

1. It is known that the middle line of a trapezoid is equal to the half-sum of its bases. The base is equal, and the base is. Then

Answer:

2. The easiest way to solve this problem is to notice that (the parallelogram rule). Calculate the coordinates of vectors and is not difficult:. When vectors are added, the coordinates are added. Then has coordinates. The point also has the same coordinates, since the origin of the vector is the point with coordinates. We are interested in the ordinate. It is equal.

Answer:

3. We act immediately according to the formula for the distance between two points:

Answer:

4. Look at the picture and tell me, between which two shapes is the shaded area "sandwiched"? It is sandwiched between two squares. Then the area of ​​the required figure is equal to the area of ​​the large square minus the area of ​​the small one. The side of the small square is a line segment connecting the points and Its length is

Then the area of ​​the small square is

We do the same with a large square: its side is a segment connecting the points and Its length is

Then the area of ​​the large square is

We find the area of ​​the required figure by the formula:

Answer:

5. If the circle has the origin of coordinates as its center and passes through a point, then its radius will be exactly equal to the length of the segment (draw a picture and you will understand why this is obvious). Let's find the length of this segment:

Answer:

6. It is known that the radius of a circle circumscribed about a rectangle is equal to half of its diagonal. Let's find the length of any of the two diagonals (after all, in a rectangle they are equal!)

Answer:

Well, have you dealt with everything? It wasn't very hard to figure it out, was it? The rule here is one - to be able to make a visual picture and simply "read" all the data from it.

We have very little left. There are literally two more points that I would like to discuss.

Let's try to solve this simple problem. Let two points and be given. Find the coordinates of the midpoint of the segment. The solution to this problem is as follows: let the point be the desired midpoint, then it has the coordinates:

That is: midpoint coordinates = arithmetic mean of the corresponding coordinates of the segment ends.

This rule is very simple and usually does not cause difficulties for students. Let's see what tasks and how it is used:

1. Nay-di-te or-di-na-tu-re-di-us from-cut, co-uni-nya-yu-shch-go point and

2. The points are the top-shi-na-mi-you-rekh-coal-no-ka. Nay-di-te or-di-na-tu points of pe-re-se-ch-niya his dia-go-na-lei.

3. Nay-di-those abs-cis-su center-tra of the circle, described-san-noy around the coal-nik-ka, the vertices of the ko-to-ro-go have co-op-di-na-you co-vet-but.

Solutions:

1. The first problem is just a classic. We act immediately to determine the middle of the segment. It has coordinates. The ordinate is.

Answer:

2. It is easy to see that the given quadrangle is a parallelogram (even a rhombus!). You yourself can prove this by calculating the lengths of the sides and comparing them with each other. What do I know about a parallelogram? Its diagonals are halved by the intersection point! Aha! So the point of intersection of the diagonals is what? This is the middle of any of the diagonals! I will choose, in particular, the diagonal. Then the point has coordinates The ordinate of the point is equal to.

Answer:

3.What is the center of the circle circumscribed about the rectangle with? It coincides with the point of intersection of its diagonals. What do you know about the diagonals of a rectangle? They are equal and the intersection point is halved. The task was reduced to the previous one. Take the diagonal, for example. Then if is the center of the circumscribed circle, then is the middle. Looking for coordinates: Abscissa is equal.

Answer:

Now practice a little yourself, I will just give the answers to each problem so that you can test yourself.

1. Nay-di-te ra-di-us of the circle, described-san-noy around the triangle, the vertices of the co-to-ro-go have co-or-di -no misters

2. Nai-di-te or-di-na-tu center-tra of the circle, described-san-noy around the triangle-nik, the vertices of ko-to-ro-go have coordinates

3. How-to-ra-di-u-sa should there be a circle with a center at the point so that it would touch the axis of abs-cissa?

4. Nay-di-te or-di-na-tu points of pe-re-seeding of the axis and from-cut, co-uni-nya-yu-shch-go point and

Answers:

Did you succeed? I really hope for it! Now - the last push. Be especially careful now. The material that I will now explain is directly related not only to simple problems on the coordinate method from the B part, but also occurs everywhere in the C2 problem.

Which of my promises have I not kept yet? Remember what operations on vectors I promised to introduce and what ones I eventually introduced? Am I sure I haven't forgotten anything? Forgot! Forgot to explain what multiplication of vectors means.

There are two ways to multiply a vector by a vector. Depending on the chosen method, we will get objects of a different nature:

The cross product is pretty tricky. How to do it and what it is for, we will discuss with you in the next article. And in this one we will focus on the dot product.

There are two ways that we can calculate it:

As you guessed, the result should be the same! So let's look at the first way first:

Dot product in terms of coordinates

Find: - common dot product notation

The formula for the calculation is as follows:

That is, the dot product = the sum of the products of the coordinates of the vectors!

Example:

Nai di te

Solution:

Let's find the coordinates of each of the vectors:

We calculate the dot product by the formula:

Answer:

See, absolutely nothing complicated!

Well, now try it yourself:

Nay-di-te scalar-noe pro-iz-ve-de-vek-to-moat and

Did you manage? Maybe you noticed a small catch? Let's check:

The coordinates of the vectors are the same as in the previous task! Answer: .

In addition to the coordinate, there is another way to calculate the dot product, namely, through the lengths of the vectors and the cosine of the angle between them:

Indicates the angle between vectors and.

That is, the dot product is equal to the product of the lengths of the vectors and the cosine of the angle between them.

Why do we need this second formula, if we have the first, which is much simpler, at least there are no cosines in it. And it is needed so that we can deduce from the first and second formulas how to find the angle between vectors!

Let Then remember the formula for the length of the vector!

Then if I substitute this data into the dot product formula, then I get:

But on the other side:

So what did you and I get? We now have a formula to calculate the angle between two vectors! Sometimes it is also written like this for brevity:

That is, the algorithm for calculating the angle between vectors is as follows:

1. Calculate the dot product in terms of coordinates
2. Find the lengths of the vectors and multiply them
3. Divide the result of point 1 by the result of point 2

Let's practice with examples:

1. Nay-di-te is the angle between the century-to-ra-mi and. Give the answer in gra-du-sakh.

2. Under the conditions of the previous problem, find the cosine between the vectors

Let's do this: I'll help you solve the first problem, and try to do the second yourself! Agree? Then let's get started!

1. These vectors are our old acquaintances. We have already counted their dot product and it was equal. Their coordinates are:,. Then we find their lengths:

Then we are looking for the cosine between the vectors:

What is the cosine of the angle? This is the corner.

Answer:

Now solve the second problem yourself, and then we will compare! I will only give you a very short solution:

2. has coordinates, has coordinates.

Let be the angle between vectors and, then

Answer:

It should be noted that problems directly on vectors and the method of coordinates in part B of the examination work are quite rare. However, the vast majority of C2 problems can be easily solved by introducing a coordinate system. So you can consider this article as the foundation, on the basis of which we will make quite cunning constructions that we will need to solve complex problems.

COORDINATES AND VECTORS. MEDIUM ROVEN

You and I continue to study the method of coordinates. In the last part, we derived a number of important formulas that allow:

1. Find vector coordinates
2. Find the length of a vector (alternatively: the distance between two points)
3. Add, subtract vectors. Multiply them by a real number
4. Find the midpoint of a line segment
5. Calculate dot product of vectors
6. Find the angle between vectors

Of course, the whole coordinate method does not fit into these 6 points. It lies at the heart of such a science as analytical geometry, which you will get acquainted with at the university. I just want to build a foundation that will allow you to solve problems in a single state. exam. We figured out the tasks of Part B in Now it's time to move to a qualitatively new level! This article will be devoted to the method for solving those problems C2, in which it would be reasonable to switch to the method of coordinates. This rationality is determined by what is required to find in the problem, and what figure is given. So, I would use the coordinate method if the questions are:

1. Find the angle between two planes
2. Find the angle between a line and a plane
3. Find the angle between two straight lines
4. Find the distance from a point to a plane
5. Find the distance from a point to a straight line
6. Find the distance from a straight line to a plane
7. Find the distance between two straight lines

If the figure given in the problem statement is a body of revolution (ball, cylinder, cone ...)

Suitable shapes for the coordinate method are:

1. Rectangular parallelepiped
2. Pyramid (triangular, quadrangular, hexagonal)

Also in my experience it is inappropriate to use the coordinate method for:

1. Finding the cross-sectional areas
2. Calculating the volume of bodies

However, it should be noted right away that three situations “unfavorable” for the method of coordinates are rather rare in practice. In most tasks, however, he can become your savior, especially if you are not very strong in three-dimensional constructions (which are sometimes quite intricate).

What are all the figures I have listed above? They are no longer flat, like, for example, a square, triangle, circle, but three-dimensional! Accordingly, we need to consider not a two-dimensional, but a three-dimensional coordinate system. It is built quite easily: just in addition to the abscissa and ordinate axes, we will introduce one more axis, the applicate axis. The figure schematically shows their relative position:

All of them are mutually perpendicular, intersect at one point, which we will call the origin. The abscissa axis, as before, will be denoted, the ordinate axis -, and the entered applicate axis -.

If earlier each point on the plane was characterized by two numbers - the abscissa and the ordinate, then each point in space is already described by three numbers - the abscissa, ordinate, applicate. For example:

Accordingly, the abscissa of the point is equal, the ordinate is, and the applicate is.

Sometimes the abscissa of a point is also called the projection of the point onto the abscissa axis, the ordinate is the projection of the point onto the ordinate axis, and the applicate is the projection of the point onto the applicate axis. Accordingly, if a point is specified, then a point with coordinates:

is called the projection of a point onto a plane

is called the projection of a point onto a plane

A natural question arises: are all formulas derived for the two-dimensional case valid in space? The answer is yes, they are fair and look the same. For a little detail. I think you already guessed for which one. We will have to add one more term to all formulas, which is responsible for the applicate axis. Namely.

1. If two points are given:, then:

• Vector coordinates:
• Distance between two points (or vector length)
• The middle of the segment has coordinates

2. If two vectors are given: and, then:

• Their dot product is:
• The cosine of the angle between vectors is:

However, space is not so simple. As you can imagine, the addition of one more coordinate introduces a significant variety in the spectrum of figures "living" in this space. And for further narration I will need to introduce some, roughly speaking, "generalization" of the straight line. This "generalization" is the plane. What do you know about a plane? Try to answer the question, what is a plane? It's very difficult to say. However, we all have an intuitive idea of ​​what it looks like:

Roughly speaking, this is a kind of endless "leaf" thrust into space. "Infinity" should be understood that the plane extends in all directions, that is, its area is equal to infinity. However, this explanation "on the fingers" does not give the slightest idea of ​​the structure of the plane. And we will be interested in it.

Let's remember one of the basic axioms of geometry:

• a straight line passes through two different points on the plane, moreover, only one:

Or its counterpart in space:

Of course, you remember how to derive the equation of a straight line from two given points, it is not at all difficult: if the first point has coordinates: and the second, then the equation of the straight line will be as follows:

You went through this in the 7th grade. In space, the equation of a straight line looks like this: let us have two points with coordinates:, then the equation of a straight line passing through them has the form:

For example, a straight line passes through the points:

How should this be understood? It should be understood as follows: a point lies on a straight line if its coordinates satisfy the following system:

We will not be very interested in the equation of a straight line, but we need to pay attention to a very important concept of the directing vector of a straight line. - any nonzero vector lying on the given line or parallel to it.

For example, both vectors are direction vectors of a straight line. Let be a point lying on a straight line, and be its direction vector. Then the equation of the straight line can be written in the following form:

Once again, I will not be very interested in the equation of a straight line, but I really need you to remember what a direction vector is! Again: it is ANY nonzero vector lying on a straight line or parallel to it.

Withdraw equation of a plane at three given points is no longer so trivial, and usually this issue is not addressed in a high school course. But in vain! This technique is vital when we use the coordinate method to solve complex problems. However, I am assuming that you are eager to learn something new? Moreover, you will be able to impress your teacher at the university when it turns out that you already know how with the methodology that is usually studied in the course of analytical geometry. So let's get started.

The equation of a plane is not too different from the equation of a straight line on a plane, namely, it has the form:

some numbers (not all equal to zero), but variables, for example: etc. As you can see, the equation of the plane is not very different from the equation of a straight line (linear function). However, remember what you and I said? We said that if we have three points that do not lie on one straight line, then the equation of the plane can be uniquely reconstructed from them. But how? I'll try to explain to you.

Since the equation of the plane has the form:

And the points belong to this plane, then when substituting the coordinates of each point into the equation of the plane, we should get the correct identity:

Thus, it becomes necessary to solve three equations even with unknowns! Dilemma! However, you can always assume that (for this you need to divide by). Thus, we get three equations with three unknowns:

However, we will not solve such a system, but write out a mysterious expression that follows from it:

Equation of a plane passing through three given points

\ [\ left | (\ begin (array) (* (20) (c)) (x - (x_0)) & ((x_1) - (x_0)) & ((x_2) - (x_0)) \\ (y - (y_0) ) & ((y_1) - (y_0)) & ((y_2) - (y_0)) \\ (z - (z_0)) & ((z_1) - (z_0)) & ((z_2) - (z_0)) \ end (array)) \ right | = 0 \]

Stop! What is this? Some very unusual module! However, the object you see in front of you has nothing to do with the module. This object is called a third-order determinant. From now on, when you deal with the method of coordinates on a plane, you will very often come across these same determinants. What is a third-order determinant? Oddly enough, this is just a number. It remains to understand what specific number we will compare with the determinant.

Let's first write down the third-order determinant in a more general form:

Where are some numbers. Moreover, by the first index we mean the line number, and by the index - the column number. For example, it means that the given number is at the intersection of the second row and the third column. Let's pose the next question: how exactly are we going to compute such a determinant? That is, what specific number will we match to it? For the determinant of the third order, there is a heuristic (visual) rule of the triangle, it looks as follows:

1. The product of the elements of the main diagonal (from the upper left corner to the lower right) the product of the elements forming the first triangle "perpendicular" to the main diagonal product of the elements forming the second triangle "perpendicular" to the main diagonal
2. The product of the elements of the side diagonal (from the upper right corner to the lower left) the product of the elements forming the first triangle "perpendicular" to the side diagonal product of the elements forming the second triangle "perpendicular" to the side diagonal
3. Then the determinant is equal to the difference between the values ​​obtained at step and

If we write all this in numbers, then we get the following expression:

Nevertheless, you do not need to memorize the calculation method in this form, it is enough to just keep the triangles in your head and the very idea of ​​what adds up to what and what is then subtracted from what).

Let's illustrate the triangle method with an example:

1. Calculate the determinant:

Let's figure out what we add and what we subtract:

The terms that come with a "plus":

This is the main diagonal: the product of the elements is

The first triangle, "perpendicular to the main diagonal: the product of the elements is

The second triangle, "perpendicular to the main diagonal: the product of the elements is

Add three numbers:

Terms that come with a "minus"

This is a side diagonal: the product of the elements is

The first triangle, "perpendicular to the side diagonal: the product of the elements is

Second triangle, "perpendicular to the side diagonal: the product of the elements is

Add three numbers:

All that remains to be done is to subtract from the sum of the plus terms the sum of the minus terms:

Thus,

As you can see, there is nothing complicated and supernatural in the calculation of determinants of the third order. It's just important to remember about triangles and not make arithmetic errors. Now try to calculate it yourself:

We check:

1. First triangle perpendicular to the main diagonal:
2. Second triangle perpendicular to the main diagonal:
3. Sum of terms with plus:
4. First triangle perpendicular to the side diagonal:
5. Second triangle perpendicular to the side diagonal:
6. Sum of terms with minus:
7. The sum of terms with a plus minus the sum of terms with a minus:

Here's a couple more determinants, calculate their values ​​yourself and compare them with the answers:

Answers:

Well, did it all coincide? Great, then you can move on! If there are difficulties, then my advice is this: on the Internet there are a bunch of programs for calculating the determinant on-line. All you need is to come up with your own determinant, calculate it yourself, and then compare it with what the program calculates. And so on until the results begin to coincide. I am sure this moment will not be long in coming!

Now let's go back to the determinant that I wrote out when I talked about the equation of a plane passing through three given points:

All you need is to calculate its value directly (using the triangles method) and set the result to zero. Naturally, since they are variables, you will get some expression that depends on them. It is this expression that will be the equation of the plane passing through three given points that do not lie on one straight line!

Let's illustrate this with a simple example:

1. Construct the equation of the plane passing through the points

We compose the determinant for these three points:

Simplifying:

Now we calculate it directly by the rule of triangles:

\ [(\ left | (\ begin (array) (* (20) (c)) (x + 3) & 2 & 6 \\ (y - 2) & 0 & 1 \\ (z + 1) & 5 & 0 \ end (array)) \ right | = \ left ((x + 3) \ right) \ cdot 0 \ cdot 0 + 2 \ cdot 1 \ cdot \ left ((z + 1) \ right) + \ left ((y - 2) \ right) \ cdot 5 \ cdot 6 -) \]

Thus, the equation of the plane passing through the points has the form:

Now try to solve one problem yourself, and then we will discuss it:

2. Find the equation of the plane passing through the points

Well, let's now discuss the solution:

We compose the determinant:

And we calculate its value:

Then the equation of the plane has the form:

Or, by reducing by, we get:

Now two tasks for self-control:

1. Construct the equation of a plane passing through three points:

Answers:

Did it all coincide? Again, if there are certain difficulties, then my advice is this: you take three points from your head (with a high degree of probability they will not lie on the same straight line), you build a plane along them. And then you check yourself online. For example, on the site:

However, with the help of determinants, we will construct not only the equation of the plane. Remember, I told you that not only the dot product is defined for vectors. There is also a vector product, as well as a mixed product. And if the dot product of two vectors is a number, then the vector product of two vectors will be a vector, and this vector will be perpendicular to the given ones:

Moreover, its module will be equal to the area of ​​the parallelogram built on the vectors and. We will need this vector to calculate the distance from a point to a straight line. How do we calculate the cross product of vectors and, if their coordinates are given? The determinant of the third order comes to our aid again. However, before I move on to the algorithm for calculating the vector product, I have to make a small lyrical digression.

This digression concerns basis vectors.

They are shown schematically in the figure:

Why do you think they are called basic? The fact is that :

Or in the picture:

The validity of this formula is obvious, because:

Vector product

Now I can start introducing the cross product:

The vector product of two vectors is a vector that is calculated according to the following rule:

Now let's give some examples of calculating a cross product:

Example 1: Find the cross product of vectors:

Solution: I compose a determinant:

And I calculate it:

Now, from writing in terms of basis vectors, I will return to the usual notation of a vector:

Thus:

Now try it.

Ready? We check:

And traditionally two tasks for control:

1. Find the cross product of the following vectors:
2. Find the cross product of the following vectors:

Answers:

Mixed product of three vectors

The last construction I need is a mixed product of three vectors. It, like a scalar one, is a number. There are two ways to calculate it. - through a determinant, - through a mixed product.

Namely, let us have three vectors:

Then the mixed product of three vectors, denoted by, can be calculated as:

1. - that is, the mixed product is the dot product of a vector by the cross product of two other vectors

For example, the mixed product of three vectors is:

Try to calculate it yourself through the cross product and make sure that the results match!

And again - two examples for an independent solution:

Answers:

Coordinate system selection

Well, now we have all the necessary foundation of knowledge to solve complex stereometric problems in geometry. However, before proceeding directly to the examples and algorithms for their solution, I believe that it will be useful to dwell on another question: how exactly choose a coordinate system for a particular figure. After all, it is the choice of the relative position of the coordinate system and the figure in space that will ultimately determine how cumbersome the calculations will be.

Let me remind you that in this section we are looking at the following shapes:

1. Rectangular parallelepiped
2. Straight prism (triangular, hexagonal ...)
3. Pyramid (triangular, quadrangular)
4. Tetrahedron (same as triangular pyramid)

For a rectangular box or cube, I recommend you the following construction:

That is, I will place the figure "in the corner". The cube and the parallelepiped are very nice shapes. For them, you can always easily find the coordinates of its vertices. For example, if (as shown in the picture)

then the coordinates of the vertices are as follows:

Of course, you don't need to remember this, but remembering how best to place a cube or rectangular parallelepiped is desirable.

Straight prism

The prism is a more harmful figure. It can be positioned in space in different ways. However, the following option seems to me the most acceptable:

Triangular prism:

That is, we place one of the sides of the triangle entirely on the axis, and one of the vertices coincides with the origin.

Hexagonal prism:

That is, one of the vertices coincides with the origin, and one of the sides lies on the axis.

Quadrangular and hexagonal pyramid:

The situation is similar to a cube: the two sides of the base are aligned with the coordinate axes, one of the vertices is aligned with the origin. The only small difficulty will be to calculate the coordinates of the point.

For a hexagonal pyramid - the same as for a hexagonal prism. The main task, again, will be in finding the coordinates of the vertex.

Tetrahedron (triangular pyramid)

The situation is very similar to the one I gave for a triangular prism: one vertex coincides with the origin, one side lies on the coordinate axis.

Well, now you and I are finally close to getting down to solving problems. From what I said at the very beginning of the article, you could draw the following conclusion: most C2 problems are divided into 2 categories: corner problems and distance problems. First, we will consider the problem of finding an angle. They, in turn, are divided into the following categories (as the difficulty increases):

Finding corners

1. Finding the angle between two straight lines
2. Finding the angle between two planes

Let's consider these tasks sequentially: start by finding the angle between two straight lines. Well, remember, haven’t you and I solved similar examples before? Remember, we already had something like that ... We were looking for an angle between two vectors. I will remind you, if two vectors are given: and, then the angle between them is found from the ratio:

Now we have a goal - to find the angle between two straight lines. Let's turn to the "flat picture":

How many angles did we get when two straight lines intersect? As many things. True, only two of them are not equal, while others are vertical to them (and therefore coincide with them). So what angle should we consider the angle between two straight lines: or? Here the rule is: the angle between two straight lines is always no more than degrees... That is, from two angles, we will always choose the angle with the smallest degree measure. That is, in this picture, the angle between two straight lines is equal. In order not to bother with finding the smallest of two angles every time, cunning mathematicians suggested using the module. Thus, the angle between two straight lines is determined by the formula:

As an attentive reader, you should have had a question: where, in fact, do we get these very numbers that we need to calculate the cosine of an angle? Answer: we will take them from the direction vectors of the straight lines! Thus, the algorithm for finding the angle between two straight lines is as follows:

1. We apply formula 1.

Or in more detail:

1. We are looking for the coordinates of the direction vector of the first straight line
2. We are looking for the coordinates of the direction vector of the second straight line
3. Calculate the modulus of their dot product
4. We are looking for the length of the first vector
5. We are looking for the length of the second vector
6. Multiplying the results from point 4 by the results from point 5
7. Divide the result of point 3 by the result of point 6. We get the cosine of the angle between the lines
8. If this result allows you to calculate the angle exactly, look for it
9. Otherwise, we write through the inverse cosine

Well, now is the time to move on to the tasks: I will demonstrate the solution of the first two in detail, I will present the solution of another one in a short form, and for the last two problems I will only give answers, you must carry out all the calculations for them yourself.

Tasks:

1. In the correct tet-ra-ed-re nay-di-those angle between you-so-that tet-ra-ed-ra and the med-di-a-noy bo-kovy face.

2. In the right-handed six-coal-noy pi-ra-mi-de, the sides of the os-no-va-nia are equal, and the ribs are equal, find the angle between the straight lines and.

3. The lengths of all the ribs of the correct four-you-rekh-coal pi-ra-mi-dy are equal to each other. Nay-di-those are the angle between the straight lines and if from-cut is you-co-that given pi-ra-mi-dy, the point is se-re-di-na her bo-ko- second rib

4. On the edge of the cube from-me-che-na point so that Nay-di-te is the angle between straight lines and

5. Point - se-re-di-on the edges of the cube Nay-di-te angle between straight lines and.

It is no coincidence that I have arranged the tasks in this order. While you have not yet had time to start navigating the method of coordinates, I myself will analyze the most "problematic" figures, and I will leave you to deal with the simplest cube! Gradually, you will have to learn how to work with all the figures; I will increase the complexity of the tasks from topic to topic.

Let's start solving problems:

1. Draw a tetrahedron, place it in the coordinate system as I suggested earlier. Since the tetrahedron is regular, all its faces (including the base) are regular triangles. Since we are not given the length of the side, I can take it equal. I think you understand that the angle will not really depend on how much our tetrahedron will be "stretched" ?. I will also draw the height and median in the tetrahedron. Along the way, I will draw its base (it will also be useful to us).

I need to find the angle between and. What do we know? We only know the coordinate of the point. This means that we still need to find the coordinates of the points. Now we think: a point is the intersection point of the heights (or bisectors or medians) of the triangle. A point is a raised point. The point is the middle of the segment. Then finally we need to find: coordinates of points:.

Let's start with the simplest: point coordinates. Look at the picture: It is clear that the applicate of the point is equal to zero (the point lies on the plane). Its ordinate is (since - the median). It is more difficult to find its abscissa. However, this is easily done based on the Pythagorean theorem: Consider a triangle. Its hypotenuse is equal, and one of the legs is equal Then:

Finally, we have:.

Now let's find the coordinates of the point. It is clear that its applicate is again equal to zero, and its ordinate is the same as that of a point, that is. Let's find its abscissa. This is done quite trivially if you remember that the heights of an equilateral triangle are divided by the point of intersection in proportion counting from the top. Since:, then the required abscissa of the point, equal to the length of the segment, is equal to:. Thus, the coordinates of the point are equal:

Let's find the coordinates of the point. It is clear that its abscissa and ordinate coincide with the abscissa and ordinate of the point. And the applicate is equal to the length of the segment. - this is one of the legs of the triangle. The hypotenuse of a triangle is a segment - a leg. It is searched for from the considerations that I have highlighted in bold:

The point is the midpoint of the line segment. Then we need to remember the formula for the coordinates of the midpoint of the segment:

That's it, now we can search for the coordinates of the direction vectors:

Well, everything is ready: we substitute all the data into the formula:

Thus,

Answer:

You should not be intimidated by such "scary" answers: for C2 problems, this is a common practice. I would rather be surprised at the "nice" answer in this part. Also, as you noticed, I practically did not resort to anything other than the Pythagorean theorem and the property of heights of an equilateral triangle. That is, to solve the stereometric problem, I used the very minimum of stereometry. The gain in this is partially "extinguished" by rather cumbersome calculations. But they are quite algorithmic!

2. Let's draw a regular hexagonal pyramid together with a coordinate system, as well as its base:

We need to find the angle between the lines and. Thus, our task is reduced to finding the coordinates of points:. We will find the coordinates of the last three from the small picture, and we will find the coordinate of the vertex through the coordinate of the point. Work in bulk, but you need to start it!

a) Coordinate: it is clear that its applicate and ordinate are equal to zero. Let's find the abscissa. To do this, consider a right-angled triangle. Alas, in it we only know the hypotenuse, which is equal to. We will try to find the leg (for it is clear that the doubled leg length will give us the abscissa of the point). How can we find her? Let's remember what kind of figure we have at the base of the pyramid? This is a regular hexagon. What does it mean? This means that it has all sides and all angles. I ought to find one such corner. Any ideas? There are a lot of ideas, but there is a formula:

The sum of the angles of a regular n-gon is .

Thus, the sum of the angles of a regular hexagon is equal to degrees. Then each of the angles is equal to:

We look at the picture again. It is clear that the segment is the bisector of the angle. Then the angle is equal to degrees. Then:

Then where.

Thus, it has coordinates

b) Now we can easily find the coordinate of the point:.

c) Find the coordinates of the point. Since its abscissa coincides with the length of the segment, it is equal to. Finding the ordinate is also not very difficult: if we connect the points and denote the intersection point of the straight line, say, by. (DIY easy construction). Then Thus, the ordinate of point B is equal to the sum of the lengths of the segments. Let's look at the triangle again. Then

Then since Then the point has coordinates

d) Now we find the coordinates of the point. Consider a rectangle and prove that Thus, the coordinates of the point are:

e) It remains to find the coordinates of the vertex. It is clear that its abscissa and ordinate coincide with the abscissa and ordinate of the point. Let's find the applicator. Since, then. Consider a right-angled triangle. By the statement of the problem, the side edge. This is the hypotenuse of my triangle. Then the height of the pyramid is the leg.

Then the point has coordinates:

All right, I have the coordinates of all points of interest to me. Looking for the coordinates of the direction vectors of straight lines:

We are looking for the angle between these vectors:

Answer:

Again, when solving this problem, I did not use any sophisticated tricks, except for the formula for the sum of the angles of a regular n-gon, as well as determining the cosine and sine of a right triangle.

3. Since we are again not given the lengths of the ribs in the pyramid, I will consider them equal to one. Thus, since ALL edges, and not only the lateral ones, are equal to each other, then at the base of the pyramid and me lies a square, and the lateral edges are regular triangles. Let's draw such a pyramid, as well as its base on a plane, marking all the data given in the text of the problem:

We are looking for the angle between and. I will be doing very brief calculations when I search for the coordinates of points. You will need to "decipher" them:

b) - the middle of the segment. Its coordinates:

c) I will find the length of the segment by the Pythagorean theorem in a triangle. I will find it in a triangle by the Pythagorean theorem.

Coordinates:

d) - the middle of the segment. Its coordinates are equal

e) Vector coordinates

f) Vector coordinates

g) Looking for an angle:

The cube is the simplest figure. I'm sure you can deal with her on your own. The answers to problems 4 and 5 are as follows:

Finding the angle between a straight line and a plane

Well, the time for simple tasks is over! Now the examples will be even more complicated. To find the angle between a straight line and a plane, we will proceed as follows:

1. From three points we construct the equation of the plane
   ,
   using a third-order determinant.
2. Looking for the coordinates of the directing vector of the straight line by two points:
3. We apply the formula to calculate the angle between a straight line and a plane:

As you can see, this formula is very similar to the one we used to find the angles between two straight lines. The structure of the right side is just the same, and on the left we are now looking for the sine, not the cosine, as before. Well, one nasty action was added - the search for the equation of the plane.

Let's not postpone solution of examples:

1. Os-no-va-no-em direct prize-we are-la-et-sy equal-poor-wen-ny triangular-nickname You-co-that prizes-we are equal. Nai di te angle between straight and flat

2. In rectangular pa-ra-le-le-pi-pe-de from the West Nay-di-te angle between straight line and plane

3. In the correct six-coal prism, all edges are equal. Nai-di-te is the angle between a straight line and a plane.

4. In the right-handed triangular pi-ra-mi-de with os-no-va-ni-it is from the west of the ribs Nay-di-te angle, ob-ra-zo-van -this flatness of os-no-va-nia and straight, pro-ho-dya-shi through the se-re-di-us of the ribs and

5. The lengths of all the ribs of the right four-corner pyramid with apex are equal to each other. Nay-di-te is the angle between a straight line and a plane, if the point is se-re-di-na bo-ko-th ribs pi-ra-mi-dy.

Again I will solve the first two problems in detail, the third - briefly, and I leave the last two for you to solve on your own. In addition, you have already dealt with triangular and quadrangular pyramids, but not with prisms yet.

Solutions:

1. Let's depict the prism, as well as its base. Let's combine it with the coordinate system and mark all the data given in the problem statement:

I apologize for some non-observance of the proportions, but for solving the problem, this, in fact, is not so important. The plane is just the "back wall" of my prism. It is easy enough to guess that the equation of such a plane has the form:

However, this can be shown directly:

Let's choose arbitrary three points on this plane: for example,.

Let's compose the equation of the plane:

An exercise for you: calculate this determinant yourself. Did you do it? Then the equation of the plane has the form:

Or simply

Thus,

To solve the example, I need to find the coordinates of the direction vector of a straight line. Since the point coincided with the origin, the coordinates of the vector will simply coincide with the coordinates of the point. To do this, we first find the coordinates of the point.

To do this, consider a triangle. Let's draw the height (it is the median and bisector) from the vertex. Since, then the ordinate of the point is equal to. In order to find the abscissa of this point, we need to calculate the length of the segment. By the Pythagorean theorem we have:

Then the point has coordinates:

A point is "raised" by a point:

Then the coordinates of the vector:

Answer:

As you can see, there is nothing fundamentally difficult in solving such problems. In fact, the process further simplifies the "straightness" of a figure such as a prism. Now let's move on to the next example:

2. Draw a parallelepiped, draw a plane and a straight line in it, and also separately draw its lower base:

First, we find the equation of the plane: Coordinates of three points lying in it:

(the first two coordinates were obtained in an obvious way, and you can easily find the last coordinate from the picture from the point). Then we compose the equation of the plane:

We calculate:

We are looking for the coordinates of the direction vector: It is clear that its coordinates coincide with the coordinates of the point, isn't it? How do I find the coordinates? These are the coordinates of the point, raised along the axis of the application by one! ... Then we are looking for the required angle:

Answer:

3. Draw a regular hexagonal pyramid, and then draw a plane and a straight line in it.

Here even drawing a plane is problematic, not to mention the solution of this problem, but the coordinate method does not care! It is in its versatility that its main advantage lies!

The plane passes through three points:. We are looking for their coordinates:

1) . Draw the coordinates for the last two points yourself. The solution to the problem with a hexagonal pyramid will come in handy for this!

2) We build the equation of the plane:

We are looking for the coordinates of the vector:. (see the triangular pyramid problem again!)

3) Looking for an angle:

Answer:

As you can see, there is nothing supernaturally difficult in these tasks. You just need to be very careful with the roots. For the last two problems, I will give only answers:

As you can see, the technique for solving problems is the same everywhere: the main task is to find the coordinates of the vertices and substitute them in some formulas. It remains for us to consider one more class of problems for calculating angles, namely:

Calculating angles between two planes

The solution algorithm will be as follows:

1. By three points, we are looking for the equation of the first plane:
2. For the other three points, we are looking for the equation of the second plane:
3. We apply the formula:

As you can see, the formula is very similar to the two previous ones, with the help of which we searched for the angles between straight lines and between a straight line and a plane. So remembering this one will not be difficult for you. Let's go straight to the analysis of tasks:

1. One hundred-ro-na of the os-but-va-nia of the right-handed triangular prism is equal, and the dia-go-nal of the big face is equal. Nay-di-those are the angle between the plane and the plane of the prism.

2. In the correct four-you-rekh-coal-noy pi-ra-mi-de, all the edges of which are equal, find the sine of the angle between the plane and the plane to-stu, pro-ho-dya-shchey through the point per-pen-di-ku-lar-but straight.

3. In the correct four-you-rekh-coal prism, the sides of the axis are equal, and the sides are equal. On the edge from-me-che-to point so that. Find the angle between the plane-to-sti-mi and

4. In the right four-corner prism, the sides of the os-no-va-nia are equal, and the side edges are equal. On the edge from-me-che-to-point so that Nay-di-te is the angle between plane-to-sti-mi and.

5. In the cube nay-di-te ko-si-nus of the angle between the plane-ko-sti-mi and

Problem solutions:

1. I draw a regular (equilateral triangle at the base) triangular prism and mark on it the planes that appear in the problem statement:

We need to find the equations of two planes: The equation of the base is trivial: you can compose the corresponding determinant by three points, but I will compose the equation at once:

Now we find the equation Point has coordinates Point - Since is the median and the height of the triangle, it is easy to find in a triangle by the Pythagorean theorem. Then the point has coordinates: Find the applicate of the point To do this, consider a right-angled triangle

Then we get the following coordinates: Make up the equation of the plane.

We calculate the angle between the planes:

Answer:

2. Making a drawing:

The most difficult thing is to understand what this mysterious plane is, passing through a point perpendicularly. Well, the main thing is what is this? The main thing is attentiveness! Indeed, the line is perpendicular. The straight line is also perpendicular. Then the plane passing through these two straight lines will be perpendicular to the straight line, and, by the way, pass through the point. This plane also goes through the top of the pyramid. Then the sought plane - And the plane has already been given to us. We are looking for the coordinates of the points.

Find the coordinate of the point through the point. From the small figure it is easy to deduce that the coordinates of the point will be as follows: What is now left to find in order to find the coordinates of the top of the pyramid? You also need to calculate its height. This is done using the same Pythagorean theorem: first, prove that (trivially from small triangles forming a square at the base). Since by condition, we have:

Now everything is ready: the coordinates of the vertex:

We compose the equation of the plane:

You are already special in calculating determinants. You can easily get:

Or else (if we multiply both parts by the root of two)

Now we find the equation of the plane:

(You have not forgotten how we get the equation of the plane, right? If you do not understand where this minus one came from, then go back to the definition of the equation of the plane! It's just always before that it turned out that the origin of coordinates belonged to my plane!)

We calculate the determinant:

(You can see that the equation of the plane coincides with the equation of the straight line passing through the points and! Think why!)

Now we calculate the angle:

We need to find the sine:

Answer:

3. A tricky question: what do you think is a rectangular prism? It's just a parallelepiped you know well! Make a drawing right away! It is even possible not to depict the base separately, there is little benefit from it here:

The plane, as we noted earlier, is written in the form of an equation:

Now we make up the plane

We immediately compose the equation of the plane:

Looking for an angle:

Now the answers to the last two problems:

Well, now is the time to take a break, because you and I are great and have done a great job!

Coordinates and vectors. Advanced level

In this article, we will discuss with you another class of problems that can be solved using the coordinate method: distance problems. Namely, we will consider the following cases:

1. Calculation of the distance between crossed lines.

I have ordered these tasks as their complexity increases. It turns out to be the easiest to find distance from point to plane, and the most difficult thing is to find distance between crossing lines... Although, of course, nothing is impossible! Let's not procrastinate and immediately proceed to the consideration of the first class of problems:

Calculating the distance from a point to a plane

What do we need to solve this problem?

1. Point coordinates

So, as soon as we get all the necessary data, we apply the formula:

You should already know how we construct the equation of the plane from the previous problems that I discussed in the last part. Let's get down to the tasks right away. The scheme is as follows: 1, 2 - I help you solve, and in some detail, 3, 4 - only the answer, you make the decision yourself and compare. Let's start!

Tasks:

1. Given a cube. The length of the edge of the cube is. Nay-di-te distance-i-ni from se-re-di-us from-cut to flat-to-sti

2. Given the right-vil-naya four-you-rekh-coal-naya pi-ra-mi-da Bo-kovoe edge of the side-ro-on of the os-no-va-nia is equal. Nay-di-those distance-i-nie from point to plane-to-sti where - se-re-di-on ribs.

3. In a right-handed triangular pi-ra-mi-de with os-no-va-ni, the bo-k-th edge is equal, and the side-ro-na is-no-va- is equal to. Nay-di-te distance-i-nye from the top to the plane.

4. In the correct six-coal prism, all edges are equal. Nay-di-te distance-i-nie from point to plane.

Solutions:

1. Draw a cube with unit edges, build a segment and a plane, denote the middle of the segment by the letter

.

First, let's start with an easy one: find the coordinates of a point. Since then (remember the coordinates of the midpoint of the segment!)

Now we compose the equation of the plane by three points

\ [\ left | (\ begin (array) (* (20) (c)) x & 0 & 1 \\ y & 1 & 0 \\ z & 1 & 1 \ end (array)) \ right | = 0 \]

Now I can start looking for distance:

2. Start again with the drawing, on which we mark all the data!

For the pyramid, it would be helpful to draw its base separately.

Even the fact that I draw like a chicken with a paw does not prevent us from easily solving this problem!

Now it's easy to find the coordinates of a point

Since the coordinates of the point, then

2. Since the coordinates of point a are the midpoint of the segment, then

We can also find the coordinates of two more points on the plane without any problems.We compose the equation of the plane and simplify it:

\ [\ left | (\ left | (\ begin (array) (* (20) (c)) x & 1 & (\ frac (3) (2)) \\ y & 0 & (\ frac (3) (2)) \\ z & 0 & (\ frac ( (\ sqrt 3)) (2)) \ end (array)) \ right |) \ right | = 0 \]

Since the point has coordinates:, then we calculate the distance:

Answer (very rare!):

Well, figured it out? It seems to me that everything here is as technical as in the examples that we considered with you in the previous part. So I am sure that if you have mastered that material, then it will not be difficult for you to solve the remaining two problems. I will just give the answers:

Calculating the distance from a straight line to a plane

In fact, there is nothing new here. How can a line and a plane be located relative to each other? They have all the possibilities: intersect, or a straight line is parallel to the plane. What do you think is the distance from a straight line to the plane with which this straight line intersects? It seems to me that it is clear here that such a distance is equal to zero. An uninteresting case.

The second case is trickier: here the distance is already nonzero. However, since the line is parallel to the plane, then each point of the line is equidistant from this plane:

Thus:

And this means that my task has been reduced to the previous one: we are looking for the coordinates of any point on a straight line, we are looking for the equation of the plane, we are calculating the distance from the point to the plane. In fact, such tasks are extremely rare in the exam. I managed to find only one problem, and the data in it was such that the coordinate method was not very applicable to it!

Now let's move on to another, much more important class of problems:

Calculating the distance of a point to a straight line

What do we need?

1. Coordinates of the point from which we are looking for the distance:

2. Coordinates of any point lying on a straight line

3. Coordinates of the directing vector of the straight line

What formula do we use?

What does the denominator of this fraction mean to you and so it should be clear: this is the length of the directing vector of a straight line. There is a very tricky numerator here! The expression means the modulus (length) of the vector product of vectors and How to calculate the cross product, we studied in the previous part of the work. Refresh your knowledge, they will be very useful to us now!

Thus, the algorithm for solving problems will be as follows:

1. We are looking for the coordinates of the point from which we are looking for the distance:

2. We are looking for the coordinates of any point on the straight line to which we are looking for the distance:

3. Build a vector

4. Build the direction vector of the straight line

5. Calculate the cross product

6. We are looking for the length of the resulting vector:

7. Calculate the distance:

We have a lot of work, and the examples will be quite complex! So now focus all your attention!

1. Dana is a right-vil-naya triangular pi-ra-mi-da with a top. One hundred-ro-na os-no-va-nia pi-ra-mi-dy is equal, you-so-that is equal. Nay-di-those distance-i-nie from the se-re-di-ny of the bo-ko-in-th edge to the straight line, where the points and are the se-re-di-ny of the edges and so-from- vet-but.

2. The lengths of the ribs and the right-angled pa-ral-le-le-pi-pe-da are equal, respectively, and Nay-di-those distance from top to straight

3. In the right-handed six-coal prism, all the edges of a swarm are equal to find-di-those distance from a point to a straight line

Solutions:

1. We make a neat drawing on which we mark all the data:

We have a lot of work with you! First, I would like to describe in words what we will be looking for and in what order:

1. Coordinates of points and

2. Point coordinates

3. Coordinates of points and

4. Coordinates of vectors and

5. Their cross product

6. The length of the vector

7. The length of the vector product

8. Distance from to

Well, we have a lot of work to do! We get down to it, rolling up our sleeves!

1. To find the coordinates of the height of the pyramid, we need to know the coordinates of the point. Its applicate is zero, and the ordinate is equal to the Abscissa, it is equal to the length of the segment. Since is the height of an equilateral triangle, it is divided in relation, counting from the top, henceforth. Finally, we got the coordinates:

Point coordinates

2. - the middle of the segment

3. - the middle of the segment

Midpoint of the segment

4.Coordinates

Vector coordinates

5. Calculate the cross product:

6. The length of the vector: the easiest way is to replace that the segment is the middle line of the triangle, which means that it is equal to half of the base. So.

7. We consider the length of the vector product:

8. Finally, we find the distance:

Phew, that's it! Honestly, the solution to this problem using traditional methods (through constructions) would be much faster. But here I have reduced everything to a ready-made algorithm! I think that the solution algorithm is clear to you? Therefore, I will ask you to solve the remaining two problems on your own. Let's compare the answers?

Again, I repeat: it is easier (faster) to solve these problems through constructions, and not resorting to the coordinate method. I have demonstrated this solution only to show you a universal method that allows you to "complete nothing".

Finally, consider the last class of problems:

Calculating the distance between crossed lines

Here the problem solving algorithm will be similar to the previous one. What we have:

3. Any vector connecting points of the first and second straight lines:

How do we find the distance between straight lines?

The formula is as follows:

The numerator is the modulus of the mixed product (we introduced it in the previous part), and the denominator is the same as in the previous formula (the modulus of the vector product of the direction vectors of the straight lines, the distance between which we are looking for).

I will remind you that

then the formula for the distance can be rewritten as:

A sort of determinant divided by a determinant! Although, to be honest, I have no time for jokes here! This formula is, in fact, very cumbersome and leads to rather complicated calculations. If I were you, I would only use it as a last resort!

Let's try to solve several problems using the above method:

1. In the correct triangular prism, all the edges are equal, find the distance between the straight lines and.

2. Given the right-vil-naya triangular prism, all the edges of the os-no-va-nia of the swarm are equal rib and se-re-di-well ribs yav-la-et-sya square-ra-tom. Nai di te distance between straight we and

I decide the first, and based on it, you decide the second!

1. Draw a prism and mark the straight lines and

Point C coordinates: then

Point coordinates

Vector coordinates

Point coordinates

Vector coordinates

Vector coordinates

\ [\ left ((B, \ overrightarrow (A (A_1)) \ overrightarrow (B (C_1))) \ right) = \ left | (\ begin (array) (* (20) (l)) (\ begin (array) (* (20) (c)) 0 & 1 & 0 \ end (array)) \\ (\ begin (array) (* (20) (c)) 0 & 0 & 1 \ end (array)) \\ (\ begin (array) (* (20) (c)) (\ frac ((\ sqrt 3)) (2)) & (- \ frac (1) (2)) & 1 \ end (array)) \ end (array)) \ right | = \ frac ((\ sqrt 3)) (2) \]

We consider the cross product between vectors and

\ [\ overrightarrow (A (A_1)) \ cdot \ overrightarrow (B (C_1)) = \ left | \ begin (array) (l) \ begin (array) (* (20) (c)) (\ overrightarrow i) & (\ overrightarrow j) & (\ overrightarrow k) \ end (array) \\\ begin (array ) (* (20) (c)) 0 & 0 & 1 \ end (array) \\\ begin (array) (* (20) (c)) (\ frac ((\ sqrt 3)) (2)) & (- \ frac (1) (2)) & 1 \ end (array) \ end (array) \ right | - \ frac ((\ sqrt 3)) (2) \ overrightarrow k + \ frac (1) (2) \ overrightarrow i \]

Now we calculate its length:

Answer:

Now try to complete the second task carefully. The answer to it will be:.

Coordinates and vectors. Brief description and basic formulas

A vector is a directed line segment. - the beginning of the vector, - the end of the vector.
The vector is denoted by or.

Absolute value vector - the length of the segment representing the vector. It is indicated as.

Vector coordinates:

,
where are the ends of the vector \ displaystyle a.

Sum of vectors:.

Product of vectors:

Dot product of vectors:

Oooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooo Therefore, we will proceed to the first section, I hope, by the end of the article I will maintain a cheerful frame of mind.

The relative position of two straight lines

The case when the audience sings along with the chorus. Two straight lines can:

1) match;

2) be parallel:;

3) or intersect at a single point:.

Help for Dummies : please remember the mathematical sign of the intersection, it will be very common. The record indicates that the line intersects with the line at a point.

How to determine the relative position of two straight lines?

Let's start with the first case:

Two straight lines coincide if and only if their corresponding coefficients are proportional, that is, there is such a number of "lambdas" that the equalities

Consider the straight lines and compose three equations from the corresponding coefficients:. It follows from each equation that, therefore, these lines coincide.

Indeed, if all the coefficients of the equation multiply by -1 (change signs), and all the coefficients of the equation reduced by 2, you get the same equation:.

The second case, when the lines are parallel:

Two straight lines are parallel if and only if their coefficients for the variables are proportional: , but.

As an example, consider two lines. We check the proportionality of the corresponding coefficients for the variables:

However, it is quite clear that.

And the third case, when the lines intersect:

Two straight lines intersect if and only if their coefficients for variables are NOT proportional, that is, there is NOT such a lambda value that the equalities are fulfilled

So, for straight lines, we compose the system:

From the first equation it follows that, and from the second equation:, therefore, the system is inconsistent(no solutions). Thus, the coefficients of the variables are not proportional.

Conclusion: lines intersect

In practical tasks, you can use the solution scheme just considered. By the way, it is very similar to the algorithm for checking vectors for collinearity, which we considered in the lesson The concept of linear (non) dependence of vectors. Basis of vectors... But there is a more civilized packaging:

Example 1

Find out the relative position of the straight lines:

Solution based on the study of direction vectors of straight lines:

a) From the equations we find the direction vectors of the straight lines: .

, so the vectors are not collinear and the lines intersect.

Just in case, I will put a stone with pointers at the crossroads:

The rest jump over the stone and follow on, straight to Kashchei the Immortal =)

b) Find the direction vectors of straight lines:

Lines have the same direction vector, which means that they are either parallel or coincide. There is no need to count the determinant here either.

Obviously, the coefficients for the unknowns are proportional, while.

Let us find out whether the equality is true:

Thus,

c) Find the direction vectors of straight lines:

Let's calculate the determinant composed of the coordinates of these vectors:
hence the direction vectors are collinear. Lines are either parallel or coincide.

The coefficient of proportionality "lambda" is easy to see directly from the ratio of collinear direction vectors. However, it can also be found through the coefficients of the equations themselves: .

Now let's find out whether the equality is true. Both free terms are zero, so:

The resulting value satisfies this equation (any number generally satisfies it).

Thus, the lines coincide.

Answer:

Very soon you will learn (or even have already learned) how to solve the considered problem orally literally in a matter of seconds. In this regard, I see no reason to offer anything for an independent solution, it is better to lay another important brick in the geometric foundation:

How to build a straight line parallel to a given one?

For ignorance of this simplest task, the Nightingale the Robber severely punishes.

Example 2

The straight line is given by the equation. Equate a parallel straight line that goes through a point.

Solution: Let's denote the unknown straight letter. What does the condition say about her? The straight line goes through the point. And if the straight lines are parallel, then it is obvious that the directing vector of the straight line "tse" is also suitable for constructing the straight line "de".

We take out the direction vector from the equation:

Answer:

The geometry of the example looks straightforward:

Analytical verification consists of the following steps:

1) We check that the lines have the same direction vector (if the equation of the line is not simplified properly, then the vectors will be collinear).

2) Check if the point satisfies the obtained equation.

Analytical review is in most cases easy to do orally. Look at the two equations, and many of you will quickly figure out the parallelism of straight lines without any drawing.

Examples for a do-it-yourself solution today will be creative. Because you still have to compete with Baba Yaga, and she, you know, is a lover of all kinds of riddles.

Example 3

Make an equation of a straight line passing through a point parallel to a straight line if

There is a rational and not very rational solution. The shortest way is at the end of the lesson.

We've worked a little with parallel lines and will come back to them later. The case of coinciding straight lines is of little interest, so consider a problem that is well known to you from the school curriculum:

How to find the intersection point of two lines?

If straight intersect at a point, then its coordinates are the solution systems of linear equations

How to find the point of intersection of lines? Solve the system.

So much for you geometric meaning of a system of two linear equations in two unknowns Are two intersecting (most often) straight lines on a plane.

Example 4

Find the point of intersection of lines

Solution: There are two ways of solving - graphical and analytical.

The graphical way is to simply draw the data lines and find out the intersection point directly from the drawing:

Here's our point:. To check, you should substitute its coordinates in each equation of the straight line, they should fit both there and there. In other words, the coordinates of a point are the solution of the system. Basically, we looked at a graphical way to solve systems of linear equations with two equations, two unknowns.

The graphical method, of course, is not bad, but there are noticeable disadvantages. No, the point is not that seventh graders decide this, the point is that it will take time to get a correct and EXACT drawing. In addition, some straight lines are not so easy to construct, and the intersection point itself may be located somewhere in the thirty kingdom outside the notebook sheet.

Therefore, it is more expedient to search for the intersection point using the analytical method. Let's solve the system:

To solve the system, the method of term-by-term addition of equations was used. To build relevant skills, visit the lesson How to solve a system of equations?

Answer:

The check is trivial - the coordinates of the intersection point must satisfy every equation in the system.

Example 5

Find the point of intersection of the lines if they intersect.

This is an example for a do-it-yourself solution. It is convenient to divide the task into several stages. The analysis of the condition suggests what is needed:
1) Make up the equation of the straight line.
2) Make up the equation of the straight line.
3) Find out the relative position of the straight lines.
4) If the lines intersect, then find the intersection point.

The development of an algorithm of actions is typical for many geometric problems, and I will focus on this repeatedly.

Full solution and answer at the end of the tutorial:

A pair of shoes has not yet been worn down, as we got to the second section of the lesson:

Perpendicular straight lines. Distance from point to line.
Angle between straight lines

Let's start with a typical and very important task. In the first part, we learned how to build a straight line parallel to this one, and now the hut on chicken legs will turn 90 degrees:

How to build a straight line perpendicular to a given one?

Example 6

The straight line is given by the equation. Equate a perpendicular line through a point.

Solution: By condition it is known that. It would be nice to find the direction vector of the straight line. Since the lines are perpendicular, the trick is simple:

From the equation "remove" the normal vector:, which will be the direction vector of the straight line.

Let us compose the equation of a straight line by a point and a direction vector:

Answer:

Let's expand the geometric sketch:

Hmmm ... Orange sky, orange sea, orange camel.

Analytical verification of the solution:

1) Take out the direction vectors from the equations and with the help dot product of vectors we come to the conclusion that the straight lines are indeed perpendicular:.

By the way, you can use normal vectors, it's even easier.

2) Check if the point satisfies the obtained equation .

The check, again, is easy to do verbally.

Example 7

Find the point of intersection of perpendicular lines if the equation is known and point.

This is an example for a do-it-yourself solution. There are several actions in the task, so it is convenient to draw up the solution point by point.

Our exciting journey continues:

Distance from point to line

Before us is a straight strip of the river and our task is to reach it by the shortest route. There are no obstacles, and the most optimal route will be movement along the perpendicular. That is, the distance from a point to a straight line is the length of a perpendicular line.

Distance in geometry is traditionally denoted by the Greek letter "ro", for example: - the distance from the point "em" to the straight line "de".

Distance from point to line expressed by the formula

Example 8

Find the distance from a point to a straight line

Solution: all that is needed is to carefully substitute the numbers into the formula and carry out the calculations:

Answer:

Let's execute the drawing:

The distance from the point to the line found is exactly the length of the red line. If you draw up a drawing on checkered paper on a scale of 1 unit. = 1 cm (2 cells), then the distance can be measured with an ordinary ruler.

Consider another task for the same blueprint:

The task is to find the coordinates of a point that is symmetrical to a point with respect to a straight line ... I propose to perform the actions yourself, but I will outline the solution algorithm with intermediate results:

1) Find a line that is perpendicular to the line.

2) Find the point of intersection of the lines: .

Both actions are covered in detail in this lesson.

3) The point is the midpoint of the line segment. We know the coordinates of the middle and one of the ends. By the formulas for the coordinates of the midpoint of the segment we find.

It will not be superfluous to check that the distance is also 2.2 units.

Difficulties here can arise in calculations, but in the tower, a micro calculator helps out great, allowing you to count ordinary fractions. Repeatedly advised, will advise and again.

How to find the distance between two parallel lines?

Example 9

Find the distance between two parallel lines

This is another example for an independent solution. Let me give you a little hint: there are infinitely many ways to solve it. Debriefing at the end of the lesson, but better try to guess for yourself, I think you managed to disperse your ingenuity quite well.

Angle between two straight lines

Every angle is a jamb:


In geometry, the angle between two straight lines is taken as the SMALLEST angle, from which it automatically follows that it cannot be obtuse. In the figure, the angle indicated by the red arc is not counted as the angle between intersecting straight lines. And his "green" neighbor is considered as such, or oppositely oriented"Crimson" corner.

If the straight lines are perpendicular, then any of the 4 angles can be taken as the angle between them.

How do angles differ? Orientation. First, the direction of the corner "scrolling" is fundamentally important. Secondly, a negatively oriented angle is written with a minus sign, for example, if.

Why did I tell you this? It seems that the usual concept of an angle can be dispensed with. The fact is that in the formulas by which we will find the angles, you can easily get a negative result, and this should not take you by surprise. An angle with a minus sign is no worse, and has a very specific geometric meaning. In the drawing, for a negative angle, be sure to indicate its orientation with an arrow (clockwise).

How to find the angle between two straight lines? There are two working formulas:

Example 10

Find the angle between straight lines

Solution and Method one

Consider two straight lines given by equations in general form:

If straight not perpendicular, then oriented the angle between them can be calculated using the formula:

Let's pay close attention to the denominator - this is exactly scalar product direction vectors of straight lines:

If, then the denominator of the formula vanishes, and the vectors will be orthogonal and straight lines are perpendicular. That is why a reservation was made about the non-perpendicularity of the straight lines in the formulation.

Based on the foregoing, it is convenient to draw up a solution in two steps:

1) Calculate the scalar product of the direction vectors of straight lines:
, so the straight lines are not perpendicular.

2) The angle between the straight lines is found by the formula:

Using the inverse function, it is easy to find the corner itself. In this case, we use the oddness of the arctangent (see. Graphs and properties of elementary functions):

Answer:

In the answer, we indicate the exact value, as well as the approximate value (preferably both in degrees and in radians), calculated using a calculator.

Well, minus, so minus, that's okay. Here's a geometric illustration:

It is not surprising that the angle turned out to have a negative orientation, because in the problem statement the first number is a straight line and the "twisting" of the angle began with it.

If you really want to get a positive angle, you need to swap the straight lines, that is, take the coefficients from the second equation , and the coefficients are taken from the first equation. In short, you need to start with a straight line .

Formula for calculating the distance from a point to a straight line on a plane

If the equation of the straight line Ax + By + C = 0 is given, then the distance from the point M (M x, M y) to the straight line can be found using the following formula

Examples of tasks for calculating the distance from a point to a straight line on a plane

Example 1.

Find the distance between the line 3x + 4y - 6 = 0 and the point M (-1, 3).

Solution. Substitute in the formula the coefficients of the straight line and the coordinates of the point

Answer: the distance from a point to a straight line is 0.6.

equation of a plane passing through points perpendicular to a vector General equation of a plane

A nonzero vector perpendicular to a given plane is called normal vector (or, in short, normal ) for this plane.

Let the coordinate space (in a rectangular coordinate system) be given:

a) point ;

b) a nonzero vector (Figure 4.8, a).

It is required to draw up an equation of a plane passing through a point perpendicular to vector End of proof.

Let us now consider various types of equations of a straight line on a plane.

1) General equation of the planeP .

It follows from the derivation of the equation that simultaneously A, B and C not equal to 0 (explain why).

The point belongs to the plane P only if its coordinates satisfy the equation of the plane. Depending on the coefficients A, B, C and D plane P occupies one position or another:

- the plane passes through the origin of the coordinate system, - the plane does not pass through the origin of the coordinate system,

- the plane is parallel to the axis X,

X,

- the plane is parallel to the axis Y,

- the plane is not parallel to the axis Y,

- the plane is parallel to the axis Z,

- the plane is not parallel to the axis Z.

Prove these statements yourself.

Equation (6) is easily derived from equation (5). Indeed, let the point lie on the plane P... Then its coordinates satisfy the equation Subtracting equation (7) from equation (5) and grouping the terms, we obtain equation (6). Consider now two vectors with coordinates respectively. From formula (6) it follows that their scalar product is equal to zero. Therefore, the vector is perpendicular to the vector.The beginning and end of the last vector are respectively at the points that belong to the plane P... Therefore, the vector is perpendicular to the plane P... Distance from point to plane P, the general equation of which is is determined by the formula The proof of this formula is completely analogous to the proof of the formula for the distance between a point and a line (see Fig. 2).
Rice. 2. To the derivation of the formula for the distance between a plane and a straight line.

Indeed, the distance d between a straight line and a plane is

where is a point lying on a plane. Hence, as in Lecture No. 11, the above formula is obtained. Two planes are parallel if their normal vectors are parallel. Hence, we obtain the condition for the parallelism of two planes Are the coefficients of the general equations of the planes. Two planes are perpendicular if their normal vectors are perpendicular, from which we obtain the condition of perpendicularity of two planes if their general equations are known

Injection f between two planes is equal to the angle between their normal vectors (see Fig. 3) and can, therefore, be calculated by the formula
Determination of the angle between the planes.

(11)

Distance from point to plane and how to find it

Distance from point to plane- the length of the perpendicular dropped from a point onto this plane. There are at least two ways to find the distance from a point to a plane: geometric and algebraic.

With the geometric method you must first understand how the perpendicular is located from point to plane: maybe it lies in some convenient plane, is the height in some convenient (or not so) triangle, or maybe this perpendicular is generally the height in some pyramid.

After this first and most difficult stage, the task breaks down into several specific planimetric tasks (perhaps in different planes).

With the algebraic method in order to find the distance from a point to a plane, you need to enter a coordinate system, find the coordinates of the point and the equation of the plane, and then apply the formula for the distance from a point to a plane.