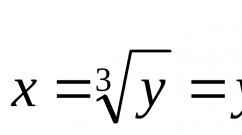Extindeți modulul x într-o serie Fourier. Matematică superioară

Multe procese care apar în natură și tehnologie tind să se repete la anumite intervale. Astfel de procese sunt numite periodice și sunt descrise matematic prin funcții periodice. Astfel de funcții includ păcat(x) , cos(x) , păcat(wx), cos(wx) . Suma a două funcții periodice, de exemplu, o funcție de forma , în general, nu mai este periodică. Dar se poate dovedi că dacă relația w 1 / w 2 este un număr rațional, atunci această sumă este o funcție periodică.

Cele mai simple procese periodice - oscilațiile armonice - sunt descrise prin funcții periodice păcat(wx) Şi cos(wx). Procesele periodice mai complexe sunt descrise de funcții compuse fie dintr-un număr finit, fie dintr-un număr infinit de termeni ai formei păcat(wx) Şi cos(wx).

3.2. Seria trigonometrică. Coeficienții Fourier

Să considerăm o serie funcțională de forma:

Această serie se numește trigonometric; numere O 0 , b 0 , o 1 , b 1 ,O 2 , b 2 …, o n , b n ,… sunt numite coeficienți serie trigonometrică. Seria (1) este adesea scrisă după cum urmează:

. (2)

Întrucât membrii seriei trigonometrice (2) au o perioadă comună
, atunci suma seriei, dacă converge, este și o funcție periodică cu perioadă
.

Să presupunem că funcția f(x) este suma acestei serii:

. (3)

În acest caz ei spun că funcția f(x) este extins într-o serie trigonometrică. Presupunând că această serie converge uniform pe interval
, puteți determina coeficienții săi folosind formulele:

,
,
. (4)

Se numesc coeficienții seriei determinate de aceste formule Coeficienții Fourier.

Se numesc seriile trigonometrice (2), ai căror coeficienți sunt determinați folosind formulele Fourier (4). lângă Fourier, corespunzător funcției f(x).

Astfel, dacă o funcție periodică f(x) este suma unei serii trigonometrice convergente, atunci această serie este seria sa Fourier.

3.3. Convergența seriei Fourier

Formulele (4) arată că coeficienții Fourier pot fi calculați pentru orice integrabil pe interval

-functie periodica, i.e. Pentru o astfel de funcție puteți construi întotdeauna o serie Fourier. Dar această serie va converge către funcție f(x) si in ce conditii?

Amintiți-vă că funcția f(x), definite pe segment [ o; b] , se numește netedă pe bucăți dacă ea și derivata sa nu au mai mult de un număr finit de puncte de discontinuitate de primul fel.

Următoarea teoremă oferă condiții suficiente pentru descompunerea unei funcții dintr-o serie Fourier.

teorema lui Dirichlet. Lasă
-functie periodica f(x) este netedă pe bucăți
. Apoi seria lui Fourier converge către f(x) în fiecare dintre punctele sale de continuitate şi la valoare 0,5(f(x+0)+ f(x-0)) la punctul de rupere.

Exemplul 1.

Extindeți funcția într-o serie Fourier f(x)= x, specificat pe interval
.

Soluţie. Această funcție satisface condițiile Dirichlet și, prin urmare, poate fi extinsă într-o serie Fourier. Folosind formulele (4) și metoda de integrare pe părți
, să găsim coeficienții Fourier:

Astfel, seria Fourier pentru funcția f(x) are o privire.

Seriile Fourier sunt o reprezentare a unei funcții arbitrare cu o anumită perioadă sub forma unei serii. ÎN vedere generală această decizie se numește descompunerea unui element pe bază ortogonală. Extinderea funcțiilor în seria Fourier este un instrument destul de puternic pentru rezolvarea diferitelor probleme datorită proprietăților acestei transformări în timpul integrării, diferențierii, precum și prin schimbarea expresiilor prin argument și convoluție.

O persoană care nu este familiarizată cu matematica superioară, precum și cu lucrările omului de știință francez Fourier, cel mai probabil nu va înțelege ce sunt aceste „serii” și pentru ce sunt necesare. Între timp, această transformare a devenit destul de integrată în viața noastră. Este folosit nu numai de matematicieni, ci și de fizicieni, chimiști, medici, astronomi, seismologi, oceanografi și mulți alții. De asemenea, să aruncăm o privire mai atentă la lucrările marelui om de știință francez care a făcut o descoperire care a fost înaintea timpului său.

Omul și transformata Fourier

Serii Fourier sunt una dintre metode (împreună cu analize și altele). Acest proces are loc de fiecare dată când o persoană aude un sunet. Urechea noastră realizează automat transformarea particule elementareîntr-un mediu elastic sunt așezate în rânduri (de-a lungul spectrului) de valori succesive ale nivelului sonor pentru tonuri de diferite înălțimi. Apoi, creierul transformă aceste date în sunete care ne sunt familiare. Toate acestea se întâmplă fără dorința sau conștiința noastră, de la sine, dar pentru a înțelege aceste procese, va fi nevoie de câțiva ani pentru a studia matematica superioară.

Mai multe despre transformata Fourier

Transformarea Fourier poate fi efectuată folosind metode analitice, numerice și alte metode. Serii Fourier se referă la metoda numerică de descompunere a oricăror procese oscilatorii - de la maree oceanice și unde luminoase la cicluri de activitate solară (și alte obiecte astronomice). Folosind aceste tehnici matematice, puteți analiza funcții, reprezentând orice procese oscilatorii ca o serie de componente sinusoidale care se deplasează de la minim la maxim și înapoi. Transformata Fourier este o funcție care descrie faza și amplitudinea sinusoidelor corespunzătoare unei anumite frecvențe. Acest proces poate fi folosit pentru a rezolva foarte multe ecuații complexe, care descriu procese dinamice care apar sub influența termică, luminoasă sau energie electrica. De asemenea, seriile Fourier fac posibilă izolarea componentelor constante în semnale oscilatorii complexe, făcând posibilă interpretarea corectă a observațiilor experimentale obținute în medicină, chimie și astronomie.

Context istoric

Părintele fondator al acestei teorii este matematicianul francez Jean Baptiste Joseph Fourier. Această transformare a fost numită ulterior după el. Inițial, omul de știință și-a folosit metoda pentru a studia și explica mecanismele conductivității termice - răspândirea căldurii în solide. Fourier a sugerat că distribuția neregulată inițială poate fi descompusă în sinusoide simple, fiecare dintre acestea având propria sa temperatura minimași maxim, precum și faza acestuia. În acest caz, fiecare astfel de componentă va fi măsurată de la minim la maxim și invers. Funcția matematică care descrie vârfurile superioare și inferioare ale curbei, precum și faza fiecăreia dintre armonici, se numește transformată Fourier a expresiei distribuției temperaturii. Autorul teoriei a reunit functia generala distribuție, care este greu de descris matematic, la o serie foarte convenabilă de cosinus și sinus, care împreună dau distribuția originală.

Principiul transformării și punctele de vedere ale contemporanilor

Contemporanii omului de știință – matematicieni de seamă de la începutul secolului al XIX-lea – nu au acceptat această teorie. Principala obiecție a fost afirmația lui Fourier că o funcție discontinuă, care descrie o linie dreaptă sau o curbă discontinuă, poate fi reprezentată ca o sumă de expresii sinusoidale care sunt continue. Ca exemplu, luați în considerare pasul Heaviside: valoarea sa este zero la stânga discontinuității și unu la dreapta. Această funcție descrie dependența curentului electric de o variabilă de timp atunci când un circuit este închis. Contemporanii teoriei de la acea vreme nu au întâlnit niciodată o situație similară în care o expresie discontinuă să fie descrisă printr-o combinație de funcții continue, obișnuite, cum ar fi exponențial, sinus, liniar sau pătratic.

Ce i-a derutat pe matematicienii francezi cu privire la teoria lui Fourier?

La urma urmei, dacă matematicianul a avut dreptate în afirmațiile sale, atunci prin însumarea seriei infinite trigonometrice Fourier, se poate obține o reprezentare precisă a expresiei pasului, chiar dacă are mulți pași similari. La începutul secolului al XIX-lea, o astfel de afirmație părea absurdă. Dar, în ciuda tuturor îndoielilor, mulți matematicieni au extins domeniul de studiu al acestui fenomen, ducându-l dincolo de studiul conductivității termice. Cu toate acestea, majoritatea oamenilor de știință au continuat să fie chinuiți de întrebarea: „Poate suma unei serii sinusoidale să convergă către valoarea exacta functie discontinua?

Convergența seriei Fourier: un exemplu

Problema convergenței se pune ori de câte ori este necesar să se însumeze serii infinite de numere. Pentru a înțelege acest fenomen, luați în considerare un exemplu clasic. Vei putea vreodată să ajungi la perete dacă fiecare pas următor este jumătate din dimensiunea celui precedent? Să presupunem că ești la doi metri de țintă, primul pas te duce până la jumătatea drumului, următorul te duce până la marcajul de trei sferturi, iar după al cincilea vei fi parcurs aproape 97 la sută din drum. Cu toate acestea, indiferent de câți pași ai face, nu îți vei atinge scopul propus într-un sens strict matematic. Folosind calcule numerice, se poate dovedi că în cele din urmă este posibil să se apropie cât mai mult de o anumită distanță. Această dovadă este echivalentă cu demonstrarea că suma unei jumătăți, a unui sfert etc. va tinde spre unitate.

Problema convergenței: a doua venire sau instrumentul lordului Kelvin

Această problemă a fost ridicată din nou la sfârșitul secolului al XIX-lea, când au încercat să folosească seria Fourier pentru a prezice intensitatea mareelor. În acest moment, Lordul Kelvin a inventat un instrument, care era un dispozitiv de calcul analogic care permitea marinarilor militari și marini comerciali să urmărească acest lucru. fenomen natural. Acest mecanism seturi determinate de faze și amplitudini dintr-un tabel de înălțimi ale mareelor ​​și puncte de timp corespunzătoare, măsurate cu atenție într-un anumit port pe tot parcursul anului. Fiecare parametru a fost o componentă sinusoidală a expresiei înălțimii mareei și a fost una dintre componentele regulate. Rezultatele măsurătorilor au fost introduse în instrumentul de calcul al lui Lord Kelvin, care a sintetizat o curbă care a prezis înălțimea apei în funcție de timp. anul viitor. Foarte curând au fost trasate curbe similare pentru toate porturile lumii.

Ce se întâmplă dacă procesul este perturbat de o funcție discontinuă?

La acea vreme părea evident că un instrument de predicție a valului mare cu un număr mare elementele contului pot calcula număr mare faze și amplitudini și astfel oferă mai mult previziuni precise. Cu toate acestea, s-a dovedit că acest model nu este observat în cazurile în care expresia mareelor ​​care ar trebui sintetizată conținea un salt ascuțit, adică era discontinuu. Dacă datele dintr-un tabel de momente de timp sunt introduse în dispozitiv, acesta calculează mai mulți coeficienți Fourier. Funcția inițială este restabilită datorită componentelor sinusoidale (în conformitate cu coeficienții aflați). Discrepanța dintre expresia originală și cea reconstruită poate fi măsurată în orice punct. Când se efectuează calcule și comparații repetate, este clar că valoarea celei mai mari erori nu scade. Cu toate acestea, ele sunt localizate în regiunea corespunzătoare punctului de discontinuitate, iar în orice alt punct tind spre zero. În 1899, acest rezultat a fost confirmat teoretic de Joshua Willard Gibbs de la Universitatea Yale.

Convergența seriilor Fourier și dezvoltarea matematicii în general

Analiza Fourier nu este aplicabilă expresiilor care conțin un număr infinit de vârfuri într-un anumit interval. În general, seria Fourier, dacă funcția inițială este reprezentată de rezultatul realului dimensiunea fizică, converg mereu. Probleme de convergență acest proces pentru clase specifice de funcții a condus la apariția de noi ramuri în matematică, de exemplu, teoria funcțiilor generalizate. Ea este asociată cu nume precum L. Schwartz, J. Mikusinski și J. Temple. În cadrul acestei teorii, un clar și precis baza teoretica sub expresii precum funcția deltă Dirac (descrie o regiune dintr-o singură zonă concentrată într-o vecinătate infinitezimală a unui punct) și „pasul” Heaviside. Datorită acestei lucrări, seria Fourier a devenit aplicabilă pentru rezolvarea ecuațiilor și a problemelor care implică concepte intuitive: sarcină punctiformă, masă punctuală, dipoli magnetici și sarcină concentrată pe un fascicul.

Metoda Fourier

Seria Fourier, în conformitate cu principiile interferenței, încep cu descompunerea formelor complexe în altele mai simple. De exemplu, o modificare a fluxului de căldură se explică prin trecerea acestuia prin diferite obstacole din material termoizolant formă neregulată sau o schimbare a suprafeței pământului - un cutremur, o schimbare a orbitei unui corp ceresc - influența planetelor. De regulă, astfel de ecuații care descriu sisteme clasice simple pot fi rezolvate cu ușurință pentru fiecare val individual. Fourier a arătat asta solutii simple poate fi însumat și pentru a obține soluții la probleme mai complexe. În termeni matematici, seriile Fourier sunt o tehnică de reprezentare a unei expresii ca o sumă de armonici - cosinus și sinus. De aceea această analiză cunoscută și sub denumirea de analiză armonică.

Seria Fourier - o tehnică ideală înainte de „era computerelor”

Înainte de creație echipamente informatice Tehnica lui Fourier a fost cea mai bună armăîn arsenalul oamenilor de știință atunci când lucrează cu natura ondulatorie a lumii noastre. Seria Fourier în formă complexă face posibilă rezolvarea nu numai sarcini simple, care sunt susceptibile de aplicarea directă a legilor mecanicii lui Newton, dar și a ecuațiilor fundamentale. Majoritatea descoperirilor științei newtoniene din secolul al XIX-lea au fost posibile doar prin tehnica lui Fourier.

Seria Fourier azi

Odată cu dezvoltarea computerelor, transformatele Fourier s-au ridicat la un nivel calitativ nou nivel. Această tehnică este ferm stabilită în aproape toate domeniile științei și tehnologiei. Un exemplu este audio și video digital. Implementarea sa a devenit posibilă doar datorită unei teorii dezvoltate de un matematician francez la începutul secolului al XIX-lea. Astfel, seria Fourier în formă complexă a făcut posibilă realizarea unei descoperiri în studiu spațiul cosmic. În plus, a influențat studiul fizicii materialelor semiconductoare și a plasmei, acustica microundelor, oceanografie, radar și seismologie.

Seria Fourier trigonometrică

În matematică, o serie Fourier este un mod de a reprezenta arbitrar funcții complexe suma celor mai simple. ÎN cazuri generale numărul de astfel de expresii poate fi infinit. Mai mult, cu cât numărul lor este luat în considerare în calcul, cu atât este mai precis. rezultatul final. Cel mai adesea folosit ca protozoare funcții trigonometrice cosinus sau sinus. În acest caz, seriile Fourier se numesc trigonometrice, iar soluția unor astfel de expresii se numește expansiune armonică. Această metodă joacă rol importantîn matematică. În primul rând, seria trigonometrică oferă un mijloc de înfățișare și, de asemenea, studierea funcțiilor, este principalul aparat al teoriei. În plus, vă permite să rezolvați o serie de probleme din fizica matematică. În cele din urmă, această teorie a contribuit la dezvoltarea unui număr de ramuri foarte importante ale științei matematice (teoria integralelor, teoria funcțiilor periodice). În plus, a servit drept punct de plecare pentru dezvoltarea următoarelor funcții ale unei variabile reale și, de asemenea, a pus bazele analizei armonice.

Seria Fourier a unei funcții periodice par f(x) cu perioada 2p conține numai termeni cosinus (adică nu conține termeni sinus) și poate include un termen constant. Prin urmare,

unde sunt coeficienții Seria Fourier,

Expansiunea seriei Fourier în sinusuri

Seria Fourier a unei funcții periodice impare f (x) cu perioada 2p conține numai termeni cu sinusuri (adică nu conține termeni cu cosinus).

Prin urmare,

unde sunt coeficienții seriei Fourier,

Seria Fourier la jumătate de ciclu

Dacă o funcție este definită pentru un interval, să spunem de la 0 la p, și nu doar de la 0 la 2p, ea poate fi extinsă într-o serie numai în sinusuri sau numai în cosinus. Seria Fourier rezultată se numește aproape Fourier pe semiciclu

Dacă vrei să obții descompunerea Fourier pe jumătate de ciclu De cosinus funcțiile f (x) în intervalul de la 0 la p, atunci este necesar să se construiască o funcție periodică pară. În fig. Mai jos este funcția f (x) = x, construită pe intervalul de la x = 0 la x = p. Deoarece funcția pare este simetrică față de axa f (x), desenăm linia AB, așa cum se arată în Fig. de mai jos. Dacă presupunem că în afara intervalului considerat s-a obţinut formă triunghiulară este periodic cu o perioadă de 2p, apoi graficul final arată ca, arată. în fig. de mai jos. Deoarece trebuie să obținem expansiunea Fourier în cosinus, ca și mai înainte, calculăm coeficienții Fourier a o și a n

Dacă trebuie să obțineți descompunere Fourier pe jumătate de ciclu De sinusurile funcțiile f (x) în intervalul de la 0 la p, atunci este necesar să se construiască o funcție periodică impară. În fig. Mai jos este funcția f (x) =x, construită pe intervalul de la x=0 la x=p. Deoarece funcția impară este simetrică față de origine, construim linia CD, așa cum se arată în Fig.

Dacă presupunem că în afara intervalului considerat semnalul dinte de ferăstrău rezultat este periodic cu o perioadă de 2p, atunci graficul final are forma prezentată în Fig. Deoarece trebuie să obținem expansiunea Fourier a semiciclului în termeni de sinusuri, ca și mai înainte, calculăm coeficientul Fourier. b

Ministerul Învățământului General și Profesional

Soci universitate de stat turism

și afaceri în stațiune

Institutul Pedagogic

Facultatea de Matematică

Departamentul de Matematică Generală

TEZĂ DE DIPLOMA

Seria Fourier și aplicațiile lor

În fizica matematică.

Completat de: student anul 5

semnătura de învățământ cu normă întreagă

Specialitatea 010100

"Matematică"

Kasperova N.S.

ID student nr. 95471

Conducător științific: conferențiar, candidat.

semnătura tehnică stiinte

Pozin P.A.

Soci, 2000

1. Introducere.

2. Conceptul de serie Fourier.

2.1. Determinarea coeficienților seriei Fourier.

2.2. Integrale ale funcțiilor periodice.

3. Semne de convergență ale seriei Fourier.

3.1. Exemple de extindere a funcțiilor în seria Fourier.

4. O notă despre extinderea seriei Fourier a unei funcții periodice

5. Serii Fourier pentru funcții pare și impare.

6. Serii Fourier pentru funcții cu perioada 2 l .

7. Expansiunea seriei Fourier a unei funcții neperiodice.

Introducere.

Jean Baptiste Joseph Fourier - matematician francez, membru al Academiei de Științe din Paris (1817).

Primele lucrări ale lui Fourier s-au referit la algebră. Deja în prelegerile din 1796 el a expus teorema numărului rădăcini adevărate ecuație algebrică situat între aceste granițe (publicat în 1820), numit după el; o soluție completă a numărului de rădăcini reale ale unei ecuații algebrice a fost obținută în 1829 de către J.S.F. Prin asalt. În 1818, Fourier a investigat problema condițiilor de aplicabilitate a metodei de soluționare numerică a ecuațiilor dezvoltată de Newton, neștiind despre rezultate similare obținute în 1768 de matematicianul francez J.R. Murailem. Rezultatul muncii lui Fourier asupra metodelor numerice de rezolvare a ecuațiilor este „Analiză anumite ecuații", publicat postum în 1831.

Principala zonă de studiu a lui Fourier a fost fizica matematică. În 1807 și 1811 a prezentat Academiei de Științe din Paris primele sale descoperiri privind teoria propagării căldurii în corp solid, iar în 1822 a publicat lucrare celebră « Teoria analitică căldură”, care a jucat un rol major în istoria ulterioară a matematicii. Aceasta - teorie matematică conductivitate termică. Datorită generalității metodei, această carte a devenit sursa tuturor metode moderne fizica matematica. În această lucrare, Fourier a derivat ecuație diferențială conductivitate termică și idei dezvoltate în cel mai mult schiță generală schițată mai devreme de D. Bernoulli, a dezvoltat o metodă de separare a variabilelor (metoda Fourier) pentru a rezolva ecuația căldurii în anumite condiții la limită date, pe care a aplicat-o într-o serie de cazuri speciale (cub, cilindru etc.). Această metodă se bazează pe reprezentarea funcțiilor prin serii Fourier trigonometrice.

Seriile Fourier au devenit acum un instrument bine dezvoltat în teoria ecuațiilor cu diferențe parțiale pentru rezolvarea problemelor cu valori la limită.

1. Conceptul de serie Fourier.(pag. 94, Uvarenkov)

Seriile Fourier joacă un rol important în fizica matematică, teoria elasticității, inginerie electrică și mai ales cazul lor special - seria Fourier trigonometrică.

O serie trigonometrică este o serie a formei

sau, simbolic:

(1)

unde ω, a 0, a 1, …, a n, …, b 0, b 1, …, b n, … sunt numere constante (ω>0).

Din punct de vedere istoric, anumite probleme din fizică au condus la studiul unor astfel de serii, de exemplu, problema vibrațiilor corzilor (secolul al XVIII-lea), problema regularităților în fenomenele de conducere a căldurii etc. În aplicații, luarea în considerare a seriei trigonometrice. , asociată în primul rând cu sarcina de a reprezenta o mișcare dată, descrisă de ecuația y = ƒ(χ), în

sub forma unei sume a celor mai simple oscilații armonice, adesea luate într-un număr infinit de mare, adică ca suma unei serii de forma (1).

Astfel, ajungem la următoarea problemă: pentru a afla dacă pentru o funcție dată ƒ(x) pe un interval dat există o serie (1) care ar converge pe acest interval către această funcție. Dacă acest lucru este posibil, atunci ei spun că în acest interval funcția ƒ(x) este extinsă într-o serie trigonometrică.

Seria (1) converge într-un punct x 0, datorită periodicității funcțiilor

(n=1,2,..), se va dovedi a fi convergent în toate punctele formei (m este orice număr întreg), și astfel suma sa S(x) va fi (în regiunea de convergență a seriei ) o funcție periodică: dacă S n ( x) este a n-a sumă parțială a acestei serii, atunci avem

şi prin urmare

, adică S(x0 +T)=S(x0). Prin urmare, vorbind despre extinderea unei funcții ƒ(x) într-o serie de forma (1), vom presupune că ƒ(x) este o funcție periodică.

2. Determinarea coeficienților de serie folosind formule Fourier.

Fie o funcție periodică ƒ(x) cu perioada 2π astfel încât să fie reprezentată printr-o serie trigonometrică convergentă către o funcție dată în intervalul (-π, π), adică este suma acestei serii:

. (2)

Să presupunem că integrala funcției din partea stângă a acestei egalități este egală cu suma integralelor termenilor acestei serii. Acest lucru va fi adevărat dacă presupunem că seria numerică compusă din coeficienții unei serii trigonometrice date este absolut convergentă, adică seria numerică pozitivă converge

(3)

Seria (1) este majorizabilă și poate fi integrată termen cu termen în intervalul (-π, π). Să integrăm ambele părți ale egalității (2):

.

Să evaluăm separat fiecare integrală care apare în partea dreaptă:

, , .

Astfel,

, unde . (4)

Estimarea coeficienților Fourier.(Bugrov)

Teorema 1. Fie ca funcția ƒ(x) a perioadei 2π să aibă o derivată continuă ƒ ( s) (x) ordin s, satisfacerea inegalității pe întreaga axă reală:

│ ƒ (s) (x)│≤ M s ; (5)

apoi coeficienții Fourier ai funcției ƒ satisface inegalitatea

(6)

Dovada. Integrarea pe părți și ținând cont de faptul că

ƒ(-π) = ƒ(π), avem

Integrarea partea dreaptă(7) în mod consecvent, ținând cont de faptul că derivatele ƒ ΄, …, ƒ (s-1) sunt continue și iau aceleasi valoriîn punctele t = -π și t = π, precum și estimarea (5), obținem prima estimare (6).

A doua estimare (6) se obține într-un mod similar.

Teorema 2. Pentru coeficienții Fourier ƒ(x) este valabilă următoarea inegalitate:

(8)

Dovada. Avem

Serii Fourier de funcții periodice cu perioada 2π.

Seria Fourier ne permite să studiem funcțiile periodice prin descompunerea lor în componente. Curenții și tensiunile alternative, deplasările, viteza și accelerația mecanismelor de manivelă și undele acustice sunt tipice exemple practice aplicarea funcţiilor periodice în calculele inginereşti.

Expansiunea seriei Fourier se bazează pe presupunerea că toate având semnificație practică funcțiile din intervalul -π ≤x≤ π pot fi exprimate sub forma unor serii trigonometrice convergente (o serie este considerată convergentă dacă șirul sumelor parțiale compuse din termenii săi converge):

Notație standard (=obișnuită) prin suma lui sinx și cosx

f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,

unde a o, a 1,a 2,...,b 1,b 2,.. sunt constante reale, i.e.

Unde, pentru intervalul de la -π la π, coeficienții seriei Fourier sunt calculați folosind formulele:

Se numesc coeficienții a o , a n și b n Coeficienții Fourier, iar dacă pot fi găsite, atunci se numește seria (1). lângă Fourier, corespunzător funcţiei f(x). Pentru seria (1), termenul (a 1 cosx+b 1 sinx) se numește primul sau armonică fundamentală,

O altă modalitate de a scrie o serie este să utilizați relația acosx+bsinx=csin(x+α)

f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)

Unde a o este o constantă, cu 1 =(a 1 2 +b 1 2) 1/2, cu n =(a n 2 +b n 2) 1/2 - amplitudinile diferitelor componente și este egal cu a n =arctg a n /b n.

Pentru seria (1), termenul (a 1 cosx+b 1 sinx) sau c 1 sin(x+α 1) se numește primul sau armonică fundamentală,(a 2 cos2x+b 2 sin2x) sau c 2 sin(2x+α 2) se numește a doua armonicăși așa mai departe.

Pentru a reprezenta cu acuratețe un semnal complex necesită de obicei un număr infinit de termeni. Cu toate acestea, în multe probleme practice este suficient să luăm în considerare doar primii termeni.

Serii Fourier de funcții neperiodice cu perioada 2π.

Extinderea funcțiilor neperiodice.

Dacă funcția f(x) este neperiodică, înseamnă că nu poate fi extinsă într-o serie Fourier pentru toate valorile lui x. Cu toate acestea, este posibil să se definească o serie Fourier reprezentând o funcție pe orice interval de lățime 2π.

Având în vedere o funcție neperiodică, o nouă funcție poate fi construită prin selectarea valorilor lui f(x) într-un anumit interval și repetându-le în afara intervalului respectiv la intervale de 2π. Deoarece noua funcție este periodică cu perioada 2π, poate fi extinsă într-o serie Fourier pentru toate valorile lui x. De exemplu, funcția f(x)=x nu este periodică. Cu toate acestea, dacă este necesar să o extindem într-o serie Fourier în intervalul de la o la 2π, atunci în afara acestui interval se construiește o funcție periodică cu o perioadă de 2π (după cum se arată în figura de mai jos).

Pentru funcțiile neperiodice, cum ar fi f(x)=x, suma seriei Fourier este egală cu valoarea lui f(x) în toate punctele dintr-un interval dat, dar nu este egală cu f(x) pentru puncte în afara intervalului. Pentru a găsi seria Fourier a unei funcții neperiodice în domeniul 2π, se folosește aceeași formulă a coeficienților Fourier.

Funcții pare și impare.

Ei spun că funcția y=f(x) chiar, dacă f(-x)=f(x) pentru toate valorile lui x. Graficele funcțiilor pare sunt întotdeauna simetrice față de axa y (adică sunt imagini în oglindă). Două exemple de funcții pare: y=x2 și y=cosx.

Ei spun că funcția y=f(x) ciudat, dacă f(-x)=-f(x) pentru toate valorile lui x. Graficele funcțiilor impare sunt întotdeauna simetrice față de origine.

Multe funcții nu sunt nici pare, nici impare.

Expansiunea seriei Fourier în cosinus.

Seria Fourier a unei funcții periodice par f(x) cu perioada 2π conține numai termeni cosinus (adică fără termeni sinus) și poate include un termen constant. Prin urmare,

unde sunt coeficienții seriei Fourier,

Seria Fourier a unei funcții periodice impare f(x) cu perioada 2π conține numai termeni cu sinusuri (adică nu conține termeni cu cosinus).

Prin urmare,

unde sunt coeficienții seriei Fourier,

Seria Fourier la jumătate de ciclu.

Dacă o funcție este definită pentru un interval, să spunem de la 0 la π, și nu doar de la 0 la 2π, ea poate fi extinsă într-o serie numai în sinusuri sau numai în cosinus. Seria Fourier rezultată se numește lângă Fourier la jumătate de ciclu.

Dacă vrei să obții descompunerea Fourier cu semiciclu prin cosinus funcțiile f(x) în intervalul de la 0 la π, atunci este necesar să se construiască o funcție periodică pară. În fig. Mai jos este funcția f(x)=x, construită pe intervalul de la x=0 la x=π. Deoarece funcția pare este simetrică față de axa f(x), desenăm linia AB, așa cum se arată în Fig. de mai jos. Dacă presupunem că în afara intervalului considerat forma triunghiulară rezultată este periodică cu o perioadă de 2π, atunci graficul final arată astfel: în fig. de mai jos. Deoarece trebuie să obținem expansiunea Fourier în cosinus, ca și mai înainte, calculăm coeficienții Fourier a o și a n

Dacă trebuie să obțineți Expansiune sinusală în semiciclu Fourier funcțiile f(x) în intervalul de la 0 la π, atunci este necesar să se construiască o funcție periodică impară. În fig. Mai jos este funcția f(x)=x, construită pe intervalul de la x=0 la x=π. Deoarece funcția impară este simetrică față de origine, construim linia CD, așa cum se arată în Fig. Dacă presupunem că în afara intervalului considerat semnalul din dinte de ferăstrău rezultat este periodic cu o perioadă de 2π, atunci graficul final are forma prezentată în Fig. Deoarece trebuie să obținem expansiunea Fourier a semiciclului în termeni de sinusuri, ca și mai înainte, calculăm coeficientul Fourier. b

Serii Fourier pentru un interval arbitrar.

Expansiunea unei funcții periodice cu perioada L.

Funcția periodică f(x) se repetă pe măsură ce x crește cu L, adică. f(x+L)=f(x). Trecerea de la funcțiile considerate anterior cu o perioadă de 2π la funcțiile cu o perioadă de L este destul de simplă, deoarece se poate face folosind o schimbare de variabilă.

Pentru a găsi seria Fourier a funcției f(x) în intervalul -L/2≤x≤L/2, introducem o nouă variabilă u astfel încât funcția f(x) să aibă o perioadă de 2π în raport cu u. Dacă u=2πx/L, atunci x=-L/2 pentru u=-π și x=L/2 pentru u=π. De asemenea, fie f(x)=f(Lu/2π)=F(u). Seria Fourier F(u) are forma

(Limitele de integrare pot fi înlocuite cu orice interval de lungime L, de exemplu, de la 0 la L)

Serii Fourier pe un semiciclu pentru funcțiile specificate în intervalul L≠2π.

Pentru substituția u=πх/L, intervalul de la x=0 la x=L corespunde intervalului de la u=0 la u=π. În consecință, funcția poate fi extinsă într-o serie numai în cosinus sau numai în sinusuri, i.e. V Seria Fourier la jumătate de ciclu.

Expansiunea cosinusului în intervalul de la 0 la L are forma