Descompunerea numerelor în factori primi, metode și exemple de descompunere. Factorizarea unui număr

Ce înseamnă factoring? Aceasta înseamnă găsirea numerelor al căror produs este egal cu numărul inițial.

Pentru a înțelege ce înseamnă factorizarea, să ne uităm la un exemplu.

Un exemplu de factorizare a unui număr

Factorizați numărul 8.

Numărul 8 poate fi reprezentat ca un produs de 2 cu 4:

Reprezentarea lui 8 ca produs de 2 * 4 înseamnă factorizare.

Rețineți că aceasta nu este singura factorizare a lui 8.

La urma urmei, 4 este factorizat astfel:

De aici pot fi reprezentate 8:

8 = 2 * 2 * 2 = 2 3

Să verificăm răspunsul nostru. Să aflăm cu ce este egală factorizarea:

Adică am primit numărul inițial, răspunsul este corect.

Factorizați numărul 24 în factori primi

Cum se descompune în factori primi numarul 24?

Un număr se numește prim dacă este divizibil doar cu unul și cu el însuși.

Numărul 8 poate fi reprezentat ca produsul lui 3 cu 8:

Aici numărul 24 este factorizat. Dar atribuirea spune „factorizați numărul 24 în factori primi”, adică. Sunt factorii principali care sunt necesari. Și în expansiunea noastră, 3 este un factor prim, iar 8 nu este un factor prim.

Ce s-a întâmplat factorizare? Acesta este un mod de a transforma un exemplu incomod și complex într-unul simplu și drăguț.) O tehnică foarte puternică! Se găsește la fiecare pas atât în ​​matematica elementară, cât și în cea superioară.

Astfel de transformări în limbajul matematic se numesc transformări identice ale expresiilor. Pentru cei care nu sunt la curent, aruncați o privire pe link. Există foarte puțin, simplu și util.) Sensul oricărei transformarea identităţii este o înregistrare a expresiei într-o altă formă păstrându-şi în acelaşi timp esenţa.

Sens factorizarea extrem de simplu si clar. Chiar de la numele în sine. Poate uitați (sau nu știți) ce este un multiplicator, dar vă puteți da seama că acest cuvânt provine de la cuvântul „înmulțire”?) Factorizarea înseamnă: reprezintă o expresie sub forma înmulțirii a ceva cu ceva. Fie ca matematica și limba rusă să mă ierte...) Atât.

De exemplu, trebuie să extindeți numărul 12. Puteți scrie în siguranță:

Așa că am prezentat numărul 12 ca o înmulțire a lui 3 cu 4. Vă rugăm să rețineți că numerele din dreapta (3 și 4) sunt complet diferite de cele din stânga (1 și 2). Dar înțelegem perfect că 12 și 3 4 unul si acelasi. Esența numărului 12 din transformare nu s-a schimbat.

Este posibil să descompun 12 diferit? Uşor!

12=3·4=2·6=3·2·2=0,5·24=........

Opțiunile de descompunere sunt nesfârșite.

Factorizarea numerelor este un lucru util. Ajută foarte mult, de exemplu, când lucrezi cu rădăcini. Dar factorizarea expresiilor algebrice nu este numai utilă, ci și necesar! Doar de exemplu:

Simplifica:

Cei care nu știu să factorizeze o expresie stau pe margine. Cei care știu cum - simplificați și obțineți:

Efectul este uimitor, nu?) Apropo, soluția este destul de simplă. Veți vedea singur mai jos. Sau, de exemplu, această sarcină:

Rezolvați ecuația:

x 5 - x 4 = 0

Se hotărăște în minte, de altfel. Folosind factorizarea. Vom rezolva acest exemplu mai jos. Răspuns: x 1 = 0; x 2 = 1.

Sau, același lucru, dar pentru cei mai în vârstă):

Rezolvați ecuația:

În aceste exemple am arătat scop principal factorizarea: simplificarea expresiilor fracţionale şi rezolvarea unor tipuri de ecuaţii. Iată o regulă generală de reținut:

Dacă avem o expresie fracțională înfricoșătoare în fața noastră, putem încerca factorizarea numărătorului și numitorului. Foarte des fracția este redusă și simplificată.

Dacă avem o ecuație în fața noastră, unde în dreapta este zero, iar în stânga - nu înțeleg ce, putem încerca să factorizăm partea stângă. Uneori ajută).

Metode de bază de factorizare.

Iată care sunt cele mai populare metode:

4. Expansiunea unui trinom pătratic.

Aceste metode trebuie reținute. Exact în acea ordine. Sunt verificate exemple complexe pentru tot moduri posibile descompunere.Și este mai bine să verificați în ordine pentru a nu vă încurca... Deci, să începem în ordine.)

1. Scoaterea factorului comun din paranteze.

Un mod simplu și de încredere. Nimic rău nu vine de la el! Se întâmplă fie bine, fie deloc.) De aceea el vine primul. Să ne dăm seama.

Toată lumea știe (cred!) regula:

a(b+c) = ab+ac

Sau, mai mult vedere generală:

a(b+c+d+.....) = ab+ac+ad+....

Toate egalitățile funcționează atât de la stânga la dreapta, cât și invers, de la dreapta la stânga. Puteți scrie:

ab+ac = a(b+c)

ab+ac+ad+.... = a(b+c+d+.....)

Acesta este scopul de a scoate factorul comun din paranteze.

Pe partea stângă O - multiplicator comun pentru toți termenii. Înmulțit cu tot ce există). În dreapta este cel mai mult O este deja localizat în afara parantezelor.

Aplicație practică Să ne uităm la metodă folosind exemple. La început opțiunea este simplă, chiar primitivă.) Dar pe această opțiune voi nota ( verde) Foarte puncte importante pentru orice factorizare.

Factorizați:

ah+9x

Care general apare multiplicatorul în ambii termeni? X, desigur! O vom scoate din paranteze. Să facem asta. Scriem imediat X în afara parantezei:

ax+9x=x(

Și în paranteze scriem rezultatul împărțirii fiecare termen chiar pe acest X. În ordine:

Asta este. Desigur, nu este nevoie să-l descriem atât de detaliat, acest lucru se face în minte. Dar este recomandabil să înțelegeți ce este). Înregistrăm în memorie:

Scriem factorul comun în afara parantezei. În paranteze scriem rezultatele împărțirii tuturor termenilor la acest factor comun. În ordine.

Deci am extins expresia ah+9x prin multiplicatori. L-am transformat în înmulțirea x cu (a+9). Observ că în expresia originală era și o înmulțire, chiar două: a·x și 9·x. Dar asta nu a fost factorizat! Pentru că pe lângă înmulțire, această expresie conținea și adunarea, semnul „+”! Și în exprimare x(a+9) Nu există altceva decât înmulțire!

Cum așa!? - Aud vocea indignată a oamenilor - Și între paranteze!?)

Da, există adăugare în paranteze. Dar trucul este că, deși parantezele nu sunt deschise, le luăm în considerare ca o singură literă.Și facem toate acțiunile cu paranteze în întregime, ca la o singură literă.În acest sens, în expresia x(a+9) Nu există nimic decât înmulțirea. Acesta este scopul factorizării.

Apropo, este posibil să verificăm cumva dacă am făcut totul corect? Uşor! Este suficient să înmulți înapoi ceea ce ai scos (x) prin paranteze și să vezi dacă a funcționat original expresie? Dacă funcționează, totul este grozav!)

x(a+9)=ax+9x

A funcționat.)

Nu există probleme în acest exemplu primitiv. Dar dacă există mai mulți termeni, și chiar cu semne diferite... Pe scurt, fiecare al treilea student da peste cap). Prin urmare:

Dacă este necesar, verificați factorizarea prin înmulțire inversă.

Factorizați:

3x+9x

Căutăm un factor comun. Ei bine, totul este clar cu X, se poate scoate. Există mai multe general factor? Da! Acesta este un trei. Puteți scrie expresia astfel:

3x+3 3x

Aici este imediat clar că factorul comun va fi 3x. Iată-l scoatem:

3ax+3 3x=3x(a+3)

Răspândește-te.

Ce se întâmplă dacă îl scoți doar x? Nimic special:

3ax+9x=x(3a+9)

Aceasta va fi, de asemenea, o factorizare. Dar, în acest proces fascinant, se obișnuiește să arăți totul la limită cât timp există o oportunitate. Aici, între paranteze, există o oportunitate de a scoate un trei. Se va dovedi:

3ax+9x=x(3a+9)=3x(a+3)

Același lucru, doar cu o acțiune suplimentară.) Rețineți:

Când scoatem factorul comun din paranteze, încercăm să scoatem maxim factor comun.

Să continuăm distracția?)

Factorizați expresia:

3akh+9х-8а-24

Ce vom lua? Trei, X? Nu... Nu poți. Vă reamintesc că nu puteți decât să scoateți general multiplicator adică în toate termenii expresiei. De aceea el general. Nu există un astfel de multiplicator aici... Ce, nu trebuie să-l extinzi!? Ei bine, da, am fost atât de fericiți... Faceți cunoștință cu:

2. Gruparea.

De fapt, este greu să numești grupul într-un mod independent factorizarea. Este mai mult o modalitate de a ieși exemplu complex.) Trebuie să grupăm termenii astfel încât totul să meargă. Acest lucru poate fi arătat doar prin exemplu. Deci, avem expresia:

3akh+9х-8а-24

Se poate observa că există câteva litere și numere comune. Dar... General nu există un multiplicator care să fie în toți termenii. Să nu ne pierdem inima și rupe expresia în bucăți. Să ne grupăm. Pentru ca fiecare piesă să aibă un factor comun, există ceva de luat. Cum îl rupem? Da, punem doar paranteze.

Permiteți-mi să vă reamintesc că parantezele pot fi plasate oriunde și oricum doriți. Doar esența exemplului nu s-a schimbat. De exemplu, puteți face acest lucru:

3akh+9х-8а-24=(3ах+9х)-(8а+24)

Vă rugăm să fiți atenți la a doua paranteză! Sunt precedate de semnul minus și 8aŞi 24 devenit pozitiv! Dacă, pentru a verifica, deschidem parantezele înapoi, semnele se vor schimba și obținem original expresie. Aceste. esența expresiei din paranteze nu s-a schimbat.

Dar dacă tocmai ați introdus paranteze fără a lua în considerare schimbarea semnului, de exemplu, așa:

3akh+9х-8а-24=(3x+9x) -(8a-24 )

ar fi o greseala. În dreapta - deja alte expresie. Deschideți parantezele și totul va deveni vizibil. Nu trebuie să decideți mai departe, da...)

Dar să revenim la factorizare. Să ne uităm la primele paranteze (3x+9x)și ne gândim, există ceva ce putem scoate? Ei bine, am rezolvat acest exemplu de mai sus, îl putem lua 3x:

(3ax+9x)=3x(a+3)

Să studiem a doua paranteză, putem adăuga un opt acolo:

(8a+24)=8(a+3)

Întreaga noastră expresie va fi:

(3ax+9x)-(8a+24)=3x(a+3)-8(a+3)

Factorizat? Nu. Rezultatul descompunerii ar trebui să fie numai inmultire dar la noi semnul minus strică totul. Dar... Ambii termeni au un factor comun! Acest (a+3). Nu degeaba am spus că toate parantezele sunt, parcă, o singură literă. Aceasta înseamnă că aceste paranteze pot fi scoase din paranteze. Da, exact așa sună.)

Facem așa cum este descris mai sus. Scriem factorul comun (a+3), în a doua paranteză scriem rezultatele împărțirii termenilor la (a+3):

3x(a+3)-8(a+3)=(a+3)(3x-8)

Toate! Nu există nimic în dreapta decât înmulțirea! Aceasta înseamnă că factorizarea a fost finalizată cu succes!) Iată:

3ax+9x-8a-24=(a+3)(3x-8)

Să repetăm ​​pe scurt esența grupului.

Dacă expresia nu general multiplicator pentru toată lumea termeni, împărțim expresia în paranteze astfel încât în ​​interiorul parantezei factorul comun a fost. O scoatem și vedem ce se întâmplă. Dacă aveți noroc și există expresii absolut identice rămase între paranteze, mutăm aceste paranteze din paranteze.

Voi adăuga că gruparea este un proces creativ). Nu merge întotdeauna de prima dată. E bine. Uneori trebuie să schimbați termeni și să luați în considerare opțiuni diferite grupuri până când este găsit unul de succes. Principalul lucru aici este să nu vă pierdeți inima!)

Exemple.

Acum, după ce te-ai îmbogățit cu cunoștințe, poți rezolva exemple dificile.) La începutul lecției au fost trei dintre acestea...

Simplifica:

În esență, am rezolvat deja acest exemplu. Fără ca noi înșine să știm.) Vă reamintesc: dacă ni se dă o fracție groaznică, încercăm să factorăm numărătorul și numitorul. Alte variante de simplificare doar nu.

Ei bine, numitorul aici nu este extins, ci numărătorul... Am extins deja numărătorul în timpul lecției! Ca aceasta:

3ax+9x-8a-24=(a+3)(3x-8)

Scriem rezultatul expansiunii în numărătorul fracției:

Conform regulii fracțiilor reducătoare (proprietatea principală a unei fracții), putem împărți (în același timp!) numărătorul și numitorul la același număr, sau expresie. Fracțiune din asta nu se schimba. Deci împărțim numărătorul și numitorul la expresie (3x-8). Și aici și colo vom obține unele. Rezultatul final al simplificării:

Aș dori să subliniez mai ales: reducerea unei fracții este posibilă dacă și numai dacă la numărător și numitor, pe lângă înmulțirea expresiilor nu este nimic. De aceea transformarea sumei (diferenței) în multiplicare atât de important pentru simplificare. Desigur, dacă expresiile diferit, atunci nimic nu va fi redus. Se va întâmpla. Dar factorizarea dă o șansă. Această șansă fără descompunere pur și simplu nu există.

Exemplu cu ecuația:

Rezolvați ecuația:

x 5 - x 4 = 0

Scoatem factorul comun x 4 din paranteze. Primim:

x 4 (x-1)=0

Ne dăm seama că produsul factorilor este egal cu zero atunci și numai atunci, când oricare dintre ele este zero. Dacă aveți îndoieli, găsiți-mi câteva numere diferite de zero care, atunci când sunt înmulțite, vor da zero.) Așa că scriem, mai întâi, primul factor:

Cu o asemenea egalitate, al doilea factor nu ne priveşte. Oricine poate fi, dar până la urmă tot va fi zero. Ce număr la puterea a patra dă zero? Numai zero! Și nici alta... Prin urmare:

Ne-am dat seama de primul factor și am găsit o rădăcină. Să ne uităm la al doilea factor. Acum nu ne mai pasă de primul factor.):

Aici am gasit o solutie: x 1 = 0; x 2 = 1. Oricare dintre aceste rădăcini se potrivește ecuației noastre.

Foarte nota importanta. Vă rugăm să rețineți că am rezolvat ecuația bucată cu bucată! Fiecare factor a fost egal cu zero, indiferent de alți factori. Apropo, dacă într-o astfel de ecuație nu sunt doi factori, ca al nostru, ci trei, cinci, câte doriți, vom rezolva exact la fel. Bucată cu bucată. De exemplu:

(x-1)(x+5)(x-3)(x+2)=0

Oricine deschide parantezele și înmulțește totul va rămâne blocat în această ecuație pentru totdeauna.) Un elev corect va vedea imediat că nu există nimic în stânga decât înmulțirea și zero în dreapta. Și va începe (în mintea lui!) să echivaleze toate parantezele pentru a ajunge la zero. Și va primi (în 10 secunde!) decizie corectă: x 1 = 1; x2 = -5; x 3 = 3; x 4 = -2.

Cool, nu?) O astfel de soluție elegantă este posibilă dacă partea stângă a ecuației factorizat. Ai indiciu?)

Ei bine, un ultim exemplu, pentru cei mai mari):

Rezolvați ecuația:

Este oarecum asemănător cu precedentul, nu crezi?) Desigur. Este timpul să ne amintim că în algebra de clasa a șaptea, sinusurile, logaritmii și orice altceva pot fi ascunse sub litere! Factorizarea funcționează pe tot parcursul matematicii.

Scoatem factorul comun lg 4 x din paranteze. Primim:

log 4 x=0

Aceasta este o singură rădăcină. Să ne uităm la al doilea factor.

Iată răspunsul final: x 1 = 1; x 2 = 10.

Sper că v-ați dat seama de puterea factorizării în simplificarea fracțiilor și rezolvarea ecuațiilor.)

În această lecție am învățat despre factoring comun și grupare. Rămâne să ne ocupăm de formulele de înmulțire prescurtată și de trinomul pătratic.

Daca va place acest site...

Apropo, mai am câteva site-uri interesante pentru tine.)

Puteți exersa rezolvarea exemplelor și puteți afla nivelul dvs. Testare cu verificare instantanee. Să învățăm - cu interes!)

Vă puteți familiariza cu funcțiile și derivatele.

Orice număr compus poate fi descompus în factori primi. Pot exista mai multe metode de descompunere. Oricare dintre metode produce același rezultat.

Cum să factorizezi un număr în factori primi în cel mai convenabil mod? Să ne uităm la cel mai bun mod de a face acest lucru folosind exemple specifice.

Exemple.

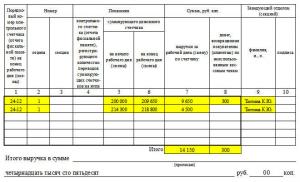
1) Factorizați numărul 1400 în factori primi.

1400 e divizibil cu 2. 2 e număr prim nu este nevoie să-l factorizezi. Obținem 700. Împărțim la 2. Obținem 350. Împărțim și 350 la 2. Numărul rezultat 175 poate fi împărțit la 5. Rezultatul este 35 - îl împărțim din nou la 5. Totalul este 7. Nu poate fi decât împărțit la 7. Obținem 1, împărțirea peste.

Același număr poate fi factorizat diferit: 1400 este împărțit convenabil la 10. 10 nu este număr prim

, deci trebuie factorizat în factori simpli: 10=2∙5. Rezultatul este 140. Împărțim din nou la 10=2∙5. Obține 14. Dacă 14 este împărțit la 14, atunci ar trebui să fie și descompus într-un produs de factori primi: 14=2∙7.

Concluzie: la descompunerea unui număr, nu este necesar să-l împărțim doar în factori primi. Împărțim la ceea ce este mai convenabil, de exemplu, la 10. Trebuie doar să vă amintiți să descompuneți divizorii compuși în factori simpli.

2) Factorizați numărul 1620 în factori primi.

Cel mai convenabil mod de a împărți numărul 1620 este la 10. Deoarece 10 nu este un număr prim, îl reprezentăm ca produs al factorilor primi: 10=2∙5. Avem 162. Este convenabil să-l împărțim la 2. Rezultatul este 81. Numărul 81 poate fi împărțit la 3, dar la 9 este mai convenabil. Deoarece 9 nu este un număr prim, îl extindem ca 9=3∙3. Obținem 9. De asemenea, îl împărțim la 9 și îl extindem în produsul factorilor primi.

Fiecare număr natural, în afară de unul, are doi sau mai mulți divizori. De exemplu, numărul 7 este divizibil fără rest doar cu 1 și 7, adică are doi divizori. Și numărul 8 are divizori 1, 2, 4, 8, adică până la 4 divizori deodată.

Care este diferența dintre numerele prime și cele compuse?

Numerele care au mai mult de doi divizori se numesc numere compuse. Numerele care au doar doi divizori: unul și numărul însuși se numesc numere prime.

Numărul 1 are o singură împărțire și anume numărul însuși. Unul nu este nici prim, nici numar compus.

• De exemplu, numărul 7 este prim, iar numărul 8 este compus.

Primele 10 numere prime: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29. Numărul 2 este singurul număr prim par, toate celelalte numere prime sunt impare.

Numărul 78 este compus, deoarece pe lângă 1 și însuși, este și divizibil cu 2. Când este împărțit la 2, obținem 39. Adică 78 = 2*39. În astfel de cazuri, se spune că numărul a fost factorizat în factori de 2 și 39.

Orice număr compus poate fi descompus în doi factori, fiecare dintre care este mai mare decât 1. Acest truc nu va funcționa cu un număr prim. Asemenea lucruri.

Factorizarea unui număr în factori primi

După cum sa menționat mai sus, orice număr compus poate fi descompus în doi factori. Să luăm, de exemplu, numărul 210. Acest număr poate fi descompus în doi factori 21 și 10. Dar numerele 21 și 10 sunt și ele compuse, să le descompunem în doi factori. Obținem 10 = 2*5, 21=3*7. Și ca rezultat, numărul 210 a fost descompus în 4 factori: 2,3,5,7. Aceste numere sunt deja prime și nu pot fi extinse. Adică am factorizat numărul 210 în factori primi.

Când se factorizează numerele compuse în factori primi, acestea sunt de obicei scrise în ordine crescătoare.

Trebuie amintit că orice număr compus poate fi descompus în factori primi și într-un mod unic, până la permutare.

• De obicei, la descompunerea unui număr în factori primi, se folosesc criterii de divizibilitate.

Să factorăm numărul 378 în factori primi

Vom nota numerele, separându-le cu o linie verticală. Numărul 378 este divizibil cu 2, deoarece se termină cu 8. Când este împărțit, obținem numărul 189. Suma cifrelor numărului 189 este divizibil cu 3, ceea ce înseamnă că numărul 189 însuși este divizibil cu 3. Rezultatul este 63.

Numărul 63 este de asemenea divizibil cu 3, în funcție de divizibilitate. Obținem 21, numărul 21 poate fi împărțit din nou la 3, obținem 7. Șapte este împărțit numai la sine, obținem unul. Aceasta completează împărțirea. În dreapta după linie sunt factorii primi în care se descompune numărul 378.

378|2
189|3
63|3
21|3

Acest articol oferă răspunsuri la întrebarea factorării unui număr pe o foaie. Să ne uităm la ideea generală de descompunere cu exemple. Să analizăm forma canonică a expansiunii și algoritmul acesteia. Toate metodele alternative vor fi luate în considerare folosind semne de divizibilitate și tabele de înmulțire.

Yandex.RTB R-A-339285-1

Ce înseamnă factorizarea unui număr în factori primi?

Să ne uităm la conceptul de factori primi. Se știe că fiecare factor prim este un număr prim. Într-un produs de forma 2 · 7 · 7 · 23 avem că avem 4 factori primi sub forma 2, 7, 7, 23.

Factorizarea presupune reprezentarea ei sub formă de produse de numere prime. Dacă trebuie să descompunăm numărul 30, atunci obținem 2, 3, 5. Intrarea va avea forma 30 = 2 · 3 · 5. Este posibil ca multiplicatorii să se repete. Un număr ca 144 are 144 = 2 2 2 2 3 3.

Nu toate numerele sunt predispuse la decădere. Numerele care sunt mai mari decât 1 și sunt numere întregi pot fi factorizate. Numerele prime, atunci când sunt factorizate, sunt divizibile doar cu 1 și cu ele însele, deci este imposibil să se reprezinte aceste numere ca un produs.

Când z se referă la numere întregi, este reprezentat ca un produs al lui a și b, unde z este împărțit la a și b. Numerele compuse sunt factorizate în factori primi folosind teorema fundamentală a aritmeticii. Dacă numărul este mai mare decât 1, atunci factorizarea lui p 1, p 2, ..., p n ia forma a = p 1 , p 2 , … , p n . Se presupune că descompunerea este într-o singură variantă.

Descompunerea canonică a unui număr în factori primi

În timpul expansiunii, factorii se pot repeta. Sunt scrise compact folosind grade. Dacă, la descompunerea numărului a, avem un factor p 1, care apare de s 1 ori și așa mai departe p n – s de n ori. Astfel expansiunea va lua forma a=p 1 s 1 · a = p 1 s 1 · p 2 s 2 · … · p n s n. Această intrare se numește factorizarea canonică a unui număr în factori primi.

Când extindem numărul 609840, obținem că 609 840 = 2 2 2 2 3 3 5 7 11 11, forma sa canonică va fi 609 840 = 2 4 3 2 5 7 11 2. Folosind extinderea canonică, puteți găsi toți divizorii unui număr și numărul lor.

Pentru a factoriza corect, trebuie să înțelegeți primul și numere compuse. Ideea este de a obține un număr succesiv de divizori de forma p 1, p 2, ..., p n numere a , a 1 , a 2 , … , a n - 1, acest lucru face posibilă obținerea a = p 1 a 1, unde a 1 = a: p 1 , a = p 1 · a 1 = p 1 · p 2 · a 2 , unde a 2 = a 1: p 2 , … , a = p 1 · p 2 · … · p n · un n , unde a n = a n - 1: p n. La primire a n = 1, apoi egalitatea a = p 1 · p 2 · … · p n obţinem descompunerea necesară a numărului a în factori primi. Rețineți că p 1 ≤ p 2 ≤ p 3 ≤ … ≤ p n.

Pentru a găsi cei mai puțin comuni factori, trebuie să utilizați un tabel cu numere prime. Acest lucru se face folosind exemplul găsirii celui mai mic divizor prim al numărului z. Când luăm numere prime 2, 3, 5, 11 și așa mai departe și împărțim numărul z la ele. Deoarece z nu este un număr prim, trebuie luat în considerare faptul că cel mai mic divizor prim nu va fi mai mare decât z. Se poate observa că nu există divizori ai lui z, atunci este clar că z este un număr prim.

Exemplul 1

Să ne uităm la exemplul numărului 87. Când este împărțit la 2, avem acel 87: 2 = 43 cu un rest de 1. Rezultă că 2 nu poate fi un divizor trebuie făcută în întregime. Când împărțim la 3, obținem 87: 3 = 29. Prin urmare, concluzia este că 3 este cel mai mic divizor prim al numărului 87.

La factorizarea în factori primi, trebuie să utilizați un tabel de numere prime, unde a. Când factorizați 95, ar trebui să utilizați aproximativ 10 numere prime, iar când factorizați 846653, aproximativ 1000.

Să luăm în considerare algoritmul de descompunere în factori primi:

• găsirea celui mai mic factor al divizorului p 1 al unui număr o prin formula a 1 = a: p 1, când a 1 = 1, atunci a este un număr prim și este inclus în descompunere, atunci când nu este egal cu 1, atunci a = p 1 · a 1 și urmați până la punctul de mai jos;
• găsirea divizorului prim p 2 al unui număr a 1 prin enumerarea succesivă a numerelor prime folosind a 2 = a 1: p 2 , când a 2 = 1 , atunci expansiunea va lua forma a = p 1 p 2 , când a 2 = 1, atunci a = p 1 p 2 a 2 , și trecem la pasul următor;
• căutarea prin numere prime și găsirea unui divizor prim p 3 numere a 2 conform formulei a 3 = a 2: p 3 când a 3 = 1 , atunci obținem că a = p 1 p 2 p 3 , când nu este egal cu 1, atunci a = p 1 p 2 p 3 a 3 și treceți la pasul următor;
• se găsește divizorul prim p n numere a n - 1 prin enumerarea numerelor prime cu pn - 1, și de asemenea a n = a n - 1: p n, unde a n = 1, pasul este final, ca rezultat obținem că a = p 1 · p 2 · … · p n .

Rezultatul algoritmului este scris sub forma unui tabel cu factori descompuse cu o bară verticală secvenţial într-o coloană. Luați în considerare figura de mai jos.

Algoritmul rezultat poate fi aplicat prin descompunerea numerelor în factori primi.

La factorizarea în factori primi, ar trebui urmat algoritmul de bază.

Exemplul 2

Factorizați numărul 78 în factori primi.

Soluţie

Pentru a găsi cel mai mic divizor prim, trebuie să parcurgeți toate numerele prime din 78. Adică 78: 2 = 39. Împărțirea fără rest înseamnă că acesta este primul divizor simplu, pe care îl notăm p 1. Obținem că a 1 = a: p 1 = 78: 2 = 39. Am ajuns la o egalitate de forma a = p 1 · a 1 , unde 78 = 2 39. Atunci un 1 = 39, adică ar trebui să trecem la pasul următor.

Să ne concentrăm pe găsirea divizorului prim p2 numere a 1 = 39. Ar trebui să parcurgeți numerele prime, adică 39: 2 = 19 (rămanând 1). Deoarece împărțirea cu rest, 2 nu este un divizor. Atunci când alegem numărul 3, obținem acel 39: 3 = 13. Aceasta înseamnă că p 2 = 3 este cel mai mic divizor prim al lui 39 cu a 2 = a 1: p 2 = 39: 3 = 13. Obținem o egalitate a formei a = p 1 p 2 a 2 sub forma 78 = 2 3 13. Avem că un 2 = 13 nu este egal cu 1, atunci ar trebui să mergem mai departe.

Cel mai mic divizor prim al numărului a 2 = 13 este găsit prin căutarea prin numere, începând cu 3. Obținem acel 13: 3 = 4 (răman de 1). Din aceasta putem observa că 13 nu este divizibil cu 5, 7, 11, deoarece 13: 5 = 2 (rest. 3), 13: 7 = 1 (rest. 6) și 13: 11 = 1 (rest. 2) . Se poate observa că 13 este un număr prim. Conform formulei, arată astfel: a 3 = a 2: p 3 = 13: 13 = 1. Am constatat că a 3 = 1, ceea ce înseamnă finalizarea algoritmului. Acum factorii se scriu ca 78 = 2 · 3 · 13 (a = p 1 · p 2 · p 3) .

Răspuns: 78 = 2 3 13.

Exemplul 3

Factorizați numărul 83.006 în factori primi.

Soluţie

Primul pas implică factoring p 1 = 2Şi a 1 = a: p 1 = 83.006: 2 = 41.503, unde 83.006 = 2 · 41.503.

Al doilea pas presupune că 2, 3 și 5 nu sunt divizori primi pentru numărul a 1 = 41.503, dar 7 este un divizor primi, deoarece 41.503: 7 = 5.929. Obținem că p 2 = 7, a 2 = a 1: p 2 = 41.503: 7 = 5.929. Evident, 83.006 = 2 7 5 929.

Aflarea celui mai mic divizor prim al lui p 4 la numărul a 3 = 847 este 7. Se poate observa că a 4 = a 3: p 4 = 847: 7 = 121, deci 83 006 = 2 7 7 7 121.

Pentru a găsi divizorul prim al numărului a 4 = 121, folosim numărul 11, adică p 5 = 11. Apoi obținem o expresie a formei a 5 = a 4: p 5 = 121: 11 = 11și 83.006 = 2 7 7 7 11 11.

Pentru număr a 5 = 11 număr p 6 = 11 este cel mai mic divizor prim. Prin urmare, a 6 = a 5: p 6 = 11: 11 = 1. Atunci a 6 = 1. Aceasta indică finalizarea algoritmului. Factorii se vor scrie ca 83 006 = 2 · 7 · 7 · 7 · 11 · 11.

Notația canonică a răspunsului va lua forma 83 006 = 2 · 7 3 · 11 2.

Răspuns: 83 006 = 2 7 7 7 11 11 = 2 7 3 11 2.

Exemplul 4

Factorizați numărul 897.924.289.

Soluţie

Pentru a găsi primul factor prim, căutați printre numerele prime, începând cu 2. Sfârșitul căutării are loc la numărul 937. Atunci p 1 = 937, a 1 = a: p 1 = 897 924 289: 937 = 958 297 și 897 924 289 = 937 958 297.

Al doilea pas al algoritmului este de a repeta peste numere prime mai mici. Adică începem cu numărul 937. Numărul 967 poate fi considerat prim deoarece este un divizor prim al numărului a 1 = 958.297. De aici obținem că p 2 = 967, apoi a 2 = a 1: p 1 = 958 297: 967 = 991 și 897 924 289 = 937 967 991.

Al treilea pas spune că 991 este un număr prim, deoarece nu are un singur factor prim care să nu depășească 991. Valoarea aproximativă a expresiei radicale este 991< 40 2 . Иначе запишем как 991 < 40 2 . Aceasta arată că p 3 = 991 și a 3 = a 2: p 3 = 991: 991 = 1. Constatăm că descompunerea numărului 897 924 289 în factori primi se obține ca 897 924 289 = 937 967 991.

Răspuns: 897 924 289 = 937 967 991.

Utilizarea testelor de divizibilitate pentru factorizarea prime

Pentru a factoriza un număr în factori primi, trebuie să urmați un algoritm. Când există numere mici, este permisă utilizarea tabelului înmulțirii și a semnelor de divizibilitate. Să ne uităm la asta cu exemple.

Exemplul 5

Dacă este necesară factorizarea 10, atunci tabelul arată: 2 · 5 = 10. Numerele rezultate 2 și 5 sunt numere prime, deci sunt factori primi pentru numărul 10.

Exemplul 6

Dacă este necesar să se descompună numărul 48, atunci tabelul arată: 48 = 6 8. Dar 6 și 8 nu sunt factori primi, deoarece ei pot fi extinși și ca 6 = 2 3 și 8 = 2 4. Apoi expansiunea completă de aici se obține ca 48 = 6 8 = 2 3 2 4. Notația canonică va lua forma 48 = 2 4 · 3.

Exemplul 7

Când descompuneți numărul 3400, puteți utiliza semnele de divizibilitate. ÎN în acest caz, Criteriile de divizibilitate cu 10 și 100 sunt relevante. De aici obținem că 3.400 = 34 · 100, unde 100 poate fi împărțit la 10, adică scris ca 100 = 10 · 10, ceea ce înseamnă că 3.400 = 34 · 10 · 10. Pe baza testului de divizibilitate, constatăm că 3 400 = 34 10 10 = 2 17 2 5 2 5. Toți factorii sunt primi. Expansiunea canonică ia forma 3 400 = 2 3 5 2 17.

Când găsim factori primi, trebuie să folosim teste de divizibilitate și tabele de înmulțire. Dacă vă imaginați numărul 75 ca un produs al factorilor, atunci trebuie să țineți cont de regula divizibilității cu 5. Obținem că 75 = 5 15 și 15 = 3 5. Adică, expansiunea dorită este un exemplu de formă a produsului 75 = 5 · 3 · 5.

Dacă observați o eroare în text, vă rugăm să o evidențiați și să apăsați Ctrl+Enter