Calculator pentru rezolvarea sistemelor de inegalități. Sisteme de inegalități liniare

Sistemul de inegalități.
Exemplul 1. Găsiți domeniul unei expresii
Soluţie. Sub semnul rădăcinii pătrate ar trebui să existe nu număr negativ, ceea ce înseamnă că două inegalități trebuie satisfăcute simultan: În astfel de cazuri, ei spun că problema se reduce la rezolvarea unui sistem de inegalități

Dar nu am întâlnit încă un astfel de model matematic (sistem de inegalități). Aceasta înseamnă că încă nu putem finaliza soluția pentru exemplu.

Inegalitățile care formează un sistem sunt combinate cu o paranteză (același lucru este valabil și în sistemele de ecuații). De exemplu, înregistrați

înseamnă că inegalitățile 2x - 1 > 3 și 3x - 2< 11 образуют систему неравенств.

Uneori un sistem de inegalități este scris sub forma unei duble inegalități. De exemplu, un sistem de inegalități

poate fi scris ca o dublă inegalitate 3<2х-1<11.

La cursul de algebră de clasa a IX-a vom lua în considerare doar sistemele a două inegalități.

Luați în considerare sistemul de inegalități

Puteți selecta mai multe dintre soluțiile sale particulare, de exemplu x = 3, x = 4, x = 3,5. De fapt, pentru x = 3 prima inegalitate ia forma 5 > 3, iar a doua ia forma 7< 11. Получились два верных числовых неравенства, значит, х = 3 - решение системы неравенств. Точно так же можно убедиться в том, что х = 4, х = 3,5 - решения системы неравенств.

În același timp, valoarea x = 5 nu este o soluție a sistemului de inegalități. Când x = 5, prima inegalitate ia forma 9 > 3 - o inegalitate numerică corectă, iar a doua ia forma 13< 11- неверное числовое неравенство .
A rezolva un sistem de inegalități înseamnă a găsi toate soluțiile sale particulare. Este clar că presupunerea demonstrată mai sus nu este o metodă de rezolvare a unui sistem de inegalități. ÎN exemplul următor Vom arăta cum raționează oamenii de obicei atunci când rezolvă un sistem de inegalități.

Exemplul 3. Rezolvați sistemul de inegalități:

Soluţie.

O) Rezolvând prima inegalitate a sistemului, găsim 2x > 4, x > 2; rezolvând a doua inegalitate a sistemului, găsim 3x< 13 Отметим эти промежутки на одной координатной прямой , использовав для выделения первого промежутка верхнюю штриховку, а для второго - нижнюю штриховку (рис. 22). Решением системы неравенств будет пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали. В рассматриваемом примере получаем интервал
b) Rezolvând prima inegalitate a sistemului, găsim x > 2; rezolvând cea de-a doua inegalitate a sistemului, găsim Să marchem aceste intervale pe o linie de coordonate, folosind hașura superioară pentru primul interval și hașura inferioară pentru al doilea (Fig. 23). Soluția sistemului de inegalități va fi intersecția soluțiilor inegalităților sistemului, i.e. intervalul în care ambele hașuri coincid. În exemplul luat în considerare obținem un fascicul

V) Rezolvând prima inegalitate a sistemului, găsim x< 2; решая второе неравенство системы, находим Отметим эти промежутки на одной координатной прямой, использовав для первого промежутка верхнюю штриховку, а для второго - нижнюю штриховку (рис. 24). Решением системы неравенств будет пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали. Здесь такого промежутка нет, значит, система неравенств не имеет решений.

Să generalizăm raționamentul efectuat în exemplul luat în considerare. Să presupunem că trebuie să rezolvăm sistemul de inegalități

Fie, de exemplu, intervalul (a, b) o soluție a inegalității fx 2 > g(x), iar intervalul (c, d) o soluție a inegalității f 2 (x) > s 2 (x ). Să marchem aceste intervale pe o linie de coordonate, folosind hașura superioară pentru primul interval și hașura inferioară pentru al doilea (Fig. 25). Soluția unui sistem de inegalități este intersecția soluțiilor inegalităților sistemului, adică. intervalul în care ambele hașuri coincid. În fig. 25 este intervalul (c, b).

Acum suntem fără munca speciala putem rezolva sistemul de inegalități pe care l-am obținut mai sus în exemplul 1:

Rezolvând prima inegalitate a sistemului, găsim x > 2; rezolvând a doua inegalitate a sistemului, găsim x< 8. Отметим эти промежутки (лучи) на одной координатной прямой, использовав для первого -верхнюю, а для второго - нижнюю штриховку (рис. 26). Решением системы неравенств будет пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали, - отрезок . Это - область определения того выражения, о котором шла речь в примере 1.

Desigur, sistemul de inegalități nu trebuie să constea neapărat din inegalități liniare, așa cum a fost cazul până acum; Pot apărea orice inegalități raționale (și nu numai raționale). Din punct de vedere tehnic, lucrul cu un sistem de inegalități raționale neliniare este, desigur, mai complicat, dar nu este nimic fundamental nou (comparativ cu sistemele de inegalități liniare) aici.

Exemplul 4. Rezolvați sistemul de inegalități

Soluţie.

1) Rezolvați inegalitatea pe care o avem
Să notăm punctele -3 și 3 pe linia numerică (Fig. 27). Ele împart linia în trei intervale, iar pe fiecare interval expresia p(x) = (x- 3)(x + 3) păstrează un semn constant - aceste semne sunt indicate în Fig. 27. Ne interesează intervalele la care inegalitatea p(x) > 0 este valabilă (sunt umbrite în Fig. 27) și punctele la care este valabilă egalitatea p(x) = 0, i.e. punctele x = -3, x = 3 (sunt marcate în Fig. 2 7 cu cearcăne). Astfel, în fig. Figura 27 prezintă un model geometric pentru rezolvarea primei inegalități.

2) Rezolvați inegalitatea pe care o avem
Să notăm punctele 0 și 5 pe linia numerică (Fig. 28). Ele împart linia în trei intervale, iar pe fiecare interval expresia<7(х) = х(5 - х) сохраняет постоянный знак - эти знаки указаны на рис. 28. Нас интересуют промежутки, на которых выполняется неравенство g(х) >O (umbrite în Fig. 28), și punctele în care egalitatea g (x) - O este satisfăcută, i.e. punctele x = 0, x = 5 (sunt marcate în Fig. 28 cu cearcăne). Astfel, în fig. Figura 28 prezintă un model geometric pentru rezolvarea celei de-a doua inegalități a sistemului.

3) Să marchem soluțiile găsite pentru prima și a doua inegalități ale sistemului pe aceeași linie de coordonate, folosind hașura superioară pentru soluțiile primei inegalități și hașura inferioară pentru soluțiile celei de-a doua (Fig. 29). Soluția sistemului de inegalități va fi intersecția soluțiilor inegalităților sistemului, i.e. intervalul în care ambele hașuri coincid. Un astfel de interval este un segment.

Exemplul 5. Rezolvați sistemul de inegalități:

Soluţie:

O) Din prima inegalitate găsim x >2. Să luăm în considerare a doua inegalitate. Trinomul pătrat x 2 + x + 2 nu are rădăcini adevărate, iar coeficientul său principal (coeficientul la x 2) este pozitiv. Aceasta înseamnă că pentru tot x inegalitatea x 2 + x + 2>0 este valabilă și, prin urmare, a doua inegalitate a sistemului nu are soluții. Ce înseamnă asta pentru sistemul de inegalități? Aceasta înseamnă că sistemul nu are soluții.

b) Din prima inegalitate găsim x > 2, iar a doua inegalitate este satisfăcută pentru orice valoare a lui x. Ce înseamnă asta pentru sistemul de inegalități? Aceasta înseamnă că soluția sa are forma x>2, adică. coincide cu soluția primei inegalități.

Răspuns:

a) fără soluții; b) x >2.

Acest exemplu este o ilustrare a următoarelor utile

1. Dacă într-un sistem de mai multe inegalități cu o variabilă o inegalitate nu are soluții, atunci sistemul nu are soluții.

2. Dacă într-un sistem de două inegalități cu o variabilă, o inegalitate este satisfăcută pentru orice valoare a variabilei, atunci soluția sistemului este soluția celei de-a doua inegalități a sistemului.

Încheind această secțiune, să revenim la problema cu privire la numărul intenționat dat la început și să o rezolvăm, după cum se spune, conform tuturor regulilor.

Exemplul 2(vezi p. 29). Destinat număr natural. Se știe că dacă adăugați 13 la pătratul numărului dorit, atunci suma va fi mai mare decât produsul numărului dorit și numărul 14. Dacă adăugați 45 la pătratul numărului dorit, atunci suma va fi fi mai putin produs numărul planificat și numărul 18. Ce număr este planificat?

Soluţie.

Prima etapă. Întocmirea unui model matematic.
Numărul intenționat x, așa cum am văzut mai sus, trebuie să satisfacă sistemul de inegalități

Etapa a doua. Lucrul cu modelul matematic compilat Să transformăm prima inegalitate a sistemului în formă
x2- 14x+ 13 > 0.

Să găsim rădăcinile trinomului x 2 - 14x + 13: x 2 = 1, x 2 = 13. Folosind parabola y = x 2 - 14x + 13 (Fig. 30) concluzionăm că inegalitatea care ne interesează este satisfăcut la x< 1 или x > 13.

Să transformăm a doua inegalitate a sistemului în forma x2 - 18 2 + 45< 0. Найдем корни трехчлена х 2 - 18x + 45: = 3, х 2 = 15.

Acest articol oferă informații inițiale despre sistemele de inegalități. Iată o definiție a unui sistem de inegalități și o definiție a unei soluții la un sistem de inegalități. Sunt enumerate și principalele tipuri de sisteme cu care cel mai adesea trebuie lucrat în lecțiile de algebră de la școală și sunt date exemple.

Navigare în pagină.

Ce este un sistem de inegalități?

Este convenabil să definim sistemele de inegalități în același mod în care am introdus definiția unui sistem de ecuații, adică prin tipul de notație și sensul încorporat în acesta.

Definiţie.

Sistemul de inegalități este o înregistrare care reprezintă un anumit număr de inegalități scrise una sub alta, unite în stânga printr-o acoladă, și denotă mulțimea tuturor soluțiilor care sunt simultan soluții la fiecare inegalitate a sistemului.

Să dăm un exemplu de sistem de inegalități. Să luăm două arbitrare, de exemplu, 2 x−3>0 și 5−x≥4 x−11, scrieți-le una sub alta
2 x−3>0 ,
5−x≥4 x−11
și se unește cu un semn de sistem - o acoladă, ca rezultat obținem un sistem de inegalități de următoarea formă:

O idee similară este dată despre sistemele de inegalități din manualele școlare. Este de remarcat faptul că definițiile lor sunt date mai restrâns: pentru inegalitățile cu o variabilă sau cu două variabile.

Principalele tipuri de sisteme de inegalități

Este clar că este posibil să se creeze infinitate sisteme diferite de inegalități. Pentru a nu te pierde în această diversitate, este indicat să-i iei în considerare în grupuri care au propriile lor caracteristici distinctive. Toate sistemele de inegalități pot fi împărțite în grupuri conform următoarelor criterii:

• prin numărul de inegalități din sistem;
• după numărul de variabile implicate în înregistrare;
• după tipul de inegalități în sine.

Pe baza numărului de inegalități incluse în evidență, se disting sisteme de doi, trei, patru etc. inegalităților În paragraful anterior am dat un exemplu de sistem, care este un sistem de două inegalități. Să arătăm un alt exemplu de sistem de patru inegalități .

Separat, vom spune că nu are rost să vorbim despre un sistem de o singură inegalitate, în acest caz, în esență despre care vorbim despre inegalitatea în sine, nu despre sistem.

Dacă te uiți la numărul de variabile, atunci există sisteme de inegalități cu unu, doi, trei etc. variabile (sau, după cum se spune și ei, necunoscute). Priviți ultimul sistem de inegalități scris la două paragrafe mai sus. Este un sistem cu trei variabile x, y și z. Vă rugăm să rețineți că primele două inegalități ale ei nu conțin toate cele trei variabile, ci doar una dintre ele. În contextul acestui sistem, ele ar trebui înțelese ca inegalități cu trei variabile de forma x+0·y+0·z≥−2 și, respectiv, 0·x+y+0·z≤5. Rețineți că școala se concentrează pe inegalitățile cu o variabilă.

Rămâne de discutat ce tipuri de inegalități sunt implicate în sistemele de înregistrare. La școală, ei iau în considerare în principal sisteme de două inegalități (mai rar - trei, chiar mai rar - patru sau mai multe) cu una sau două variabile, iar inegalitățile în sine sunt de obicei inegalități întregi gradul I sau II (mai rar - mai mult grade înalte sau fracționat rațional). Dar nu fi surprins dacă în materialele de pregătire pentru examenul de stat unificat întâlniți sisteme de inegalități care conțin inegalități iraționale, logaritmice, exponențiale și alte inegalități. Ca exemplu, dăm sistemul de inegalități , este luat din .

Care este soluția unui sistem de inegalități?

Să introducem o altă definiție legată de sistemele de inegalități - definiția unei soluții la un sistem de inegalități:

Definiţie.

Rezolvarea unui sistem de inegalități cu o variabilă se numește o astfel de valoare a unei variabile care transformă fiecare dintre inegalitățile sistemului în adevărată, cu alte cuvinte, este o soluție a fiecărei inegalități a sistemului.

Să explicăm cu un exemplu. Să luăm un sistem de două inegalități cu o variabilă. Să luăm valoarea variabilei x egală cu 8, este o soluție a sistemului nostru de inegalități prin definiție, deoarece înlocuirea sa în inegalitățile sistemului dă două inegalități numerice corecte 8>7 și 2−3·8≤0. Dimpotrivă, unitatea nu este o soluție a sistemului, deoarece atunci când este înlocuită cu variabila x, prima inegalitate se va transforma în inegalitatea numerică incorectă 1>7.

În mod similar, se poate introduce definiția unei soluții la un sistem de inegalități cu doi, trei și un număr mare variabile:

Definiţie.

Rezolvarea unui sistem de inegalități cu doi, trei etc. variabile numit pereche, trei etc. valorile acestor variabile, care în același timp este o soluție la fiecare inegalitate a sistemului, adică transformă fiecare inegalitate a sistemului într-o inegalitate numerică corectă.

De exemplu, o pereche de valori x=1, y=2 sau într-o altă notație (1, 2) este o soluție a unui sistem de inegalități cu două variabile, deoarece 1+2<7 и 1−2<0 - верные числовые неравенства. А пара (3,5, 3) не является решением этой системы, так как второе неравенство при этих значениях переменных дает неверное числовое неравенство 3,5−3<0 .

Sistemele de inegalități pot să nu aibă soluții, pot avea un număr finit de soluții sau pot avea un număr infinit de soluții. Oamenii vorbesc adesea despre setul de soluții la un sistem de inegalități. Când un sistem nu are soluții, atunci există un set gol al soluțiilor sale. Când există un număr finit de soluții, atunci mulțimea de soluții conține un număr finit de elemente, iar când există infinit de soluții, atunci mulțimea de soluții este formată dintr-un număr infinit de elemente.

Unele surse introduc definiții ale unei soluții particulare și generale a unui sistem de inegalități, ca, de exemplu, în manualele lui Mordkovich. Sub soluție privată a sistemului de inegalitățiînțelege-i o singură decizie. La rândul său soluție generală a sistemului de inegalități- acestea sunt toate deciziile ei private. Cu toate acestea, acești termeni au sens numai atunci când este necesar să subliniem în mod specific despre ce fel de soluție vorbim, dar de obicei acest lucru este deja clar din context, deci mult mai des ei spun pur și simplu „o soluție la un sistem de inegalități”.

Din definițiile unui sistem de inegalități și ale soluțiilor sale introduse în acest articol, rezultă că o soluție a unui sistem de inegalități este intersecția mulțimilor de soluții ale tuturor inegalităților acestui sistem.

Referințe.

1. Algebră: manual pentru clasa a VIII-a. educatie generala instituții / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; editat de S. A. Teliakovsky. - Ed. a XVI-a. - M.: Educație, 2008. - 271 p. : bolnav. - ISBN 978-5-09-019243-9.
2. Algebră: Clasa a IX-a: educațională. pentru invatamantul general instituții / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; editat de S. A. Teliakovsky. - Ed. a XVI-a. - M.: Educație, 2009. - 271 p. : bolnav. - ISBN 978-5-09-021134-5.
3. Mordkovich A.G. Algebră. clasa a IX-a. În 2 ore. Partea 1. Manual pentru studenții instituțiilor de învățământ general / A. G. Mordkovich, P. V. Semenov. - Ed. a XIII-a, șters. - M.: Mnemosyne, 2011. - 222 p.: ill. ISBN 978-5-346-01752-3.
4. Mordkovich A.G. Algebra și începuturile analizei matematice. clasa a XI-a. În 2 ore. Partea 1. Manual pentru studenții instituțiilor de învățământ general (nivel de profil) / A. G. Mordkovich, P. V. Semenov. - Ed. a II-a, șters. - M.: Mnemosyne, 2008. - 287 p.: ill. ISBN 978-5-346-01027-2.
5. Examenul de stat unificat-2013. Matematică: opțiuni standard de examen: 30 opțiuni / ed. A. L. Semenova, I. V. Iascenko. – M.: Editura „Educația Națională”, 2012. – 192 p. – (USE-2013. FIPI - școală).

O inegalitate este două numere sau expresii matematice legate prin unul dintre semnele: > (mai mare decât, în cazul inegalităților stricte),< (меньше, в случае строгих неравенств), ≥ (больше или равно, в случае нестрогих неравенств), ≤ (меньше или равно, в случае нестрогих неравенств).

Inegalitatea este liniarîn aceleași condiții ca și ecuația: conține variabile doar până la gradul I și nu conține produse ale variabilelor.

Soluția inegalităților liniare și a sistemelor de inegalități liniare este indisolubil legată de semnificația lor geometrică: soluția unei inegalități liniare este un anumit semiplan în care întregul plan este împărțit printr-o dreaptă, a cărei ecuație definește inegalitatea liniară. . Acest semiplan și, în cazul unui sistem de inegalități liniare, partea de plan limitată de mai multe drepte, trebuie găsite în desen.

Multe probleme economice, în special, problemele de programare liniară, în care se cere găsirea maximului sau minimului unei funcții, se reduc la rezolvarea sistemelor de inegalități liniare cu un număr mare de variabile.

Rezolvarea sistemelor de inegalități liniare cu orice număr de necunoscute

Mai întâi, să ne uităm la inegalitățile liniare din plan. Se consideră o inegalitate cu două variabile și:

,

unde sunt coeficienții variabilelor (unele numere), este termenul liber (și un număr).

O inegalitate cu două necunoscute, ca o ecuație, are un număr infinit de soluții. Soluția acestei inegalități este o pereche de numere care satisfac această inegalitate. Din punct de vedere geometric, setul de soluții la o inegalitate este reprezentat ca un semiplan delimitat de o linie dreaptă

,

pe care o vom numi linia de hotar.

Pasul 1. Construiți o dreaptă care mărginește mulțimea de soluții la o inegalitate liniară

Pentru a face acest lucru, trebuie să cunoașteți oricare două puncte de pe această linie. Să găsim punctele de intersecție cu axele de coordonate. ordonata de intersectie O egal cu zero (Figura 1). Valorile numerice de pe axele din această figură se referă la exemplul 1, pe care îl vom analiza imediat după această excursie teoretică.

Găsim abscisa rezolvând ecuația dreptei cu ecuația axei ca sistem.

Să găsim intersecția cu axa:

Înlocuind valoarea în prima ecuație, obținem

Unde .

Astfel, am găsit abscisa punctului O .

Să găsim coordonatele punctului de intersecție cu axa.

Puncte de abscisă B egal cu zero. Să rezolvăm ecuația liniei de limită cu ecuația axei de coordonate:

,

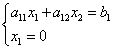
prin urmare, coordonatele punctului B: .

Pasul 2. Desenați o linie dreaptă limitând setul de soluții la inegalitate. Cunoscând punctele OŞi B intersectia liniei de limita cu axele de coordonate, putem trasa aceasta linie. O linie dreaptă (din nou Figura 1) împarte întregul plan în două părți situate la dreapta și la stânga (deasupra și dedesubt) acestei linii drepte.

Pasul 3. Determinați care semiplan este soluția acestei inegalități. Pentru a face acest lucru, trebuie să înlocuiți originea coordonatelor (0; 0) în această inegalitate. Dacă coordonatele originii satisfac inegalitatea, atunci soluția inegalității este semiplanul în care se află originea coordonatelor. Dacă coordonatele nu satisfac inegalitatea, atunci soluția inegalității este un semiplan care nu conține originea. Semiplanul soluției inegalității va fi notat cu lovituri din linie dreaptă în semiplan, ca în figura 1.

Dacă rezolvăm un sistem de inegalități liniare, apoi fiecare pas este efectuat pentru fiecare dintre inegalitățile sistemului.

Exemplul 1. Rezolvați inegalitatea

Soluţie. Să tragem o linie dreaptă

Înlocuind o dreaptă în ecuație, obținem , iar înlocuind , obținem . Prin urmare, coordonatele punctelor de intersecție cu axele vor fi O(3; 0) , B(0; 2). Să tragem o linie dreaptă prin aceste puncte (din nou, Figura 1).

Să alegem un semiplan de soluții ale inegalității. Pentru a face acest lucru, înlocuim coordonatele originii (0; 0) în inegalitatea:

obținem , adică coordonatele originii satisfac această inegalitate. În consecință, soluția inegalității este semiplanul care conține originea coordonatelor, adică semiplanul stâng (alias inferior).

Dacă această inegalitate ar fi strictă, adică ar avea forma

atunci punctele liniei de frontieră nu ar fi o soluție, deoarece nu satisfac inegalitatea.

Acum luați în considerare un sistem de inegalități liniare cu două necunoscute:

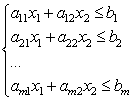
Fiecare dintre inegalitățile acestui sistem pe plan definește un semiplan. Un sistem de inegalități liniare se numește consistent dacă are cel puțin o soluție și inconsecvent dacă nu are soluții. O soluție a unui sistem de inegalități liniare este orice pereche de numere () care satisface toate inegalitățile sistemului dat.

Din punct de vedere geometric, soluția unui sistem de inegalități liniare este mulțimea de puncte care satisfac toate inegalitățile sistemului, adică partea comună a semiplanurilor rezultate. Prin urmare, geometric, în cazul general, soluția poate fi reprezentată sub forma unui poligon într-un caz particular, poate fi o linie, un segment sau chiar un punct; Dacă un sistem de inegalități liniare este inconsecvent, atunci nu există un singur punct pe plan care să satisfacă toate inegalitățile sistemului.

Exemplul 2.

Soluţie. Deci, trebuie să găsim un poligon de soluții la acest sistem de inegalități. Să construim o linie de limită pentru prima inegalitate, adică o linie, și o linie de limită pentru a doua inegalitate, adică o linie.

Facem acest lucru pas cu pas, așa cum s-a arătat în referința teoretică și în exemplul 1, mai ales că în exemplul 1 am construit o linie de limită pentru inegalitate, care este prima din acest sistem.

Semiplanurile soluțiilor corespunzătoare inegalităților acestui sistem sunt umbrite în interior în Figura 2. Partea comună a semiplanurilor soluției este un unghi deschis ABC. Aceasta înseamnă că setul de puncte din plan care formează un unghi deschis ABC, este o soluție atât pentru prima cât și pentru a doua inegalități ale sistemului, adică este o soluție pentru un sistem de două inegalități liniare. Cu alte cuvinte, coordonatele oricărui punct din această mulțime satisfac ambele inegalități ale sistemului.

Exemplul 3. Rezolvați un sistem de inegalități liniare

Soluţie. Să construim linii de limită corespunzătoare inegalităților sistemului. Facem acest lucru urmând pașii dați în ajutorul teoretic pentru fiecare inegalitate. Acum determinăm semiplanurile soluțiilor pentru fiecare inegalitate (Figura 3).

Semiplanurile soluțiilor corespunzătoare inegalităților unui sistem dat sunt umbrite spre interior. Intersecția semiplanurilor soluțiilor este reprezentată, așa cum se arată în figură, sub forma unui patrulater ABCE. Am constatat că poligonul soluțiilor unui sistem de inegalități liniare cu două variabile este un patrulater ABCE .

Tot ceea ce este descris mai sus despre sistemele de inegalități liniare cu două necunoscute se aplică și sistemelor de inegalități cu orice număr de necunoscute, cu singura diferență că soluția inegalității cu n necunoscutele vor fi totalitatea n numere () care satisfac toate inegalitățile, iar în locul liniei de graniță va exista un hiperplan de graniță n-spaţiul dimensional. Soluția va fi un poliedru de soluție (simplex) mărginit de hiperplane.

În articol vom lua în considerare rezolvarea inegalităților. Vă vom spune clar despre cum se construiește o soluție la inegalități, cu exemple clare!

Înainte de a ne uita la rezolvarea inegalităților folosind exemple, să înțelegem conceptele de bază.

Informații generale despre inegalități

Inegalitate este o expresie în care funcțiile sunt legate prin semne de relație >, . Inegalitățile pot fi atât numerice, cât și literale.
Inegalitățile cu două semne ale raportului se numesc dublu, cu trei - triplu etc. De exemplu:
a(x) > b(x),
a(x) a(x) b(x),
a(x) b(x).
a(x) Inegalitățile care conțin semnul > sau sau - nu sunt stricte.
Rezolvarea inegalității este orice valoare a variabilei pentru care această inegalitate va fi adevărată.
"Rezolvați inegalitatea" înseamnă că trebuie să găsim setul tuturor soluțiilor sale. Există diferite metode de rezolvare a inegalităților. Pentru soluții pentru inegalități Ei folosesc linia numerică, care este infinită. De exemplu, soluție la inegalitate x > 3 este intervalul de la 3 la +, iar numărul 3 nu este inclus în acest interval, prin urmare punctul de pe linie este notat cu un cerc gol, deoarece inegalitatea este strictă.
+
Răspunsul va fi: x (3; +).
Valoarea x=3 nu este inclusă în setul de soluții, deci paranteza este rotundă. Semnul infinitului este întotdeauna evidențiat cu o paranteză. Semnul înseamnă „apartenere”.
Să ne uităm la cum să rezolvăm inegalitățile folosind un alt exemplu cu semn:
x 2
-+
Valoarea x=2 este inclusă în setul de soluții, deci paranteza este pătrată, iar punctul de pe linie este indicat printr-un cerc umplut.
Răspunsul va fi: x " title=" Redat de QuickLaTeX.com">!}

Pentru a rezolva un sistem, aveți nevoie de fiecare dintre inegalitățile sale constitutive. Doar că s-a luat decizia de a nu scrie separat, ci împreună, combinându-le cu bretele.

În fiecare dintre inegalitățile sistemului, mutăm necunoscutele într-o parte, pe cele cunoscute în cealaltă cu semnul opus:

Title="Redată de QuickLaTeX.com">!}

După simplificare, ambele părți ale inegalității trebuie împărțite la numărul din fața lui X. Împărțim prima inegalitate la număr pozitiv, deci semnul inegalității nu se schimbă. Împărțim a doua inegalitate la un număr negativ, deci semnul inegalității trebuie inversat:

Title="Redată de QuickLaTeX.com">!}

Marcăm soluția inegalităților pe dreptele numerice:

Ca răspuns, notăm intersecția soluțiilor, adică partea în care există umbrire pe ambele linii.

Răspuns: x∈[-2;1).

În prima inegalitate, să scăpăm de fracție. Pentru a face acest lucru, înmulțim ambele părți termen cu termen cu cel mai mic numitor comun 2. Când este înmulțit cu un număr pozitiv, semnul inegalității nu se modifică.

În a doua inegalitate deschidem parantezele. Produsul sumei și diferența dintre două expresii este egal cu diferența pătratelor acestor expresii. În partea dreaptă este pătratul diferenței dintre cele două expresii.

Title="Redată de QuickLaTeX.com">!}

Mutăm necunoscutele într-o parte, pe cele cunoscute în cealaltă cu semnul opus și simplificăm:

Împărțim ambele părți ale inegalității la numărul din fața lui X. În prima inegalitate, împărțim la un număr negativ, deci semnul inegalității este inversat. În al doilea, împărțim la un număr pozitiv, semnul inegalității nu se schimbă:

Title="Redată de QuickLaTeX.com">!}

Ambele inegalități au semnul „mai puțin decât” (nu contează că un semn este strict „mai mic decât”, celălalt este liber, „mai mic decât sau egal”). Nu putem marca ambele soluții, dar folosim regula „ “. Cel mai mic este 1, prin urmare sistemul se reduce la inegalitate

Marcăm soluția sa pe linia numerică:

Răspuns: x∈(-∞;1].

Deschiderea parantezelor. În prima inegalitate - . Este egală cu suma cuburilor acestor expresii.

În al doilea, produsul sumei și diferența a două expresii, care este egal cu diferența de pătrate. Deoarece aici există un semn minus în fața parantezelor, este mai bine să le deschideți în două etape: mai întâi utilizați formula și abia apoi deschideți parantezele, schimbând semnul fiecărui termen în opus.

Mutăm necunoscutele într-o direcție, cunoscutele în cealaltă cu semnul opus:

Title="Redată de QuickLaTeX.com">!}

Ambele sunt mai mari decât semnele. Folosind regula „mai mult decât mai mult”, reducem sistemul de inegalități la o singură inegalitate. Cel mai mare dintre cele două numere este 5, prin urmare,

Title="Redată de QuickLaTeX.com">!}

Marcăm soluția inegalității pe dreapta numerică și notăm răspunsul:

Răspuns: x∈(5;∞).

Deoarece în sistemele algebre de inegalități liniare apar nu numai ca sarcini independente, ci și în cursul rezolvării diverse feluri ecuații, inegalități etc., este important să stăpânești acest subiect din timp.

Data viitoare ne vom uita la exemple de rezolvare a sistemelor de inegalități liniare în cazuri speciale când una dintre inegalități nu are soluții sau soluția ei este orice număr.