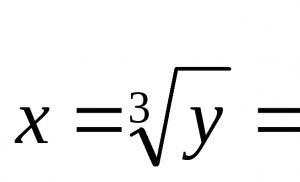Ters fonksiyon kavramı. Karşılıklı ters fonksiyonlar, temel tanımlar, özellikler, grafikler Ters fonksiyon nasıl oluşturulur

$X$ ve $Y$ kümeleri reel sayılar kümesine dahil edilsin. Tersinir fonksiyon kavramını tanıtalım.

Tanım 1

Bir $X$ kümesini bir $Y$ kümesine eşleyen $f:X\to Y$ işlevine, herhangi bir öğe için $x_1,x_2\in X$ olması durumunda, $x_1\ne x_2$ takip ettiği gerçeğinden dolayı tersinir denir. bu $f(x_1 )\ne f(x_2)$.

Artık ters fonksiyon kavramını tanıtabiliriz.

Tanım 2

$f:X\to Y$ fonksiyonunun, $X$ kümesini $Y$ kümesine eşlemesinin tersinir olmasına izin verin. Daha sonra $f^(-1):Y\to X$ işlevi, $Y$ kümesini $f^(-1)\left(y\right)=x$ koşuluyla tanımlanan $X$ kümesine eşler: $f( x)$'ın tersi denir.

Teoremi formüle edelim:

Teorem 1

$y=f(x)$ fonksiyonunun monoton olarak artan (azalan) ve belirli bir $X$ aralığında sürekli olarak tanımlandığını varsayalım. Daha sonra bu fonksiyonun değerlerinin karşılık gelen $Y$ aralığında, aynı zamanda monoton olarak artan (azalan) ve $Y$ aralığında sürekli olan ters bir fonksiyona sahiptir.

Şimdi doğrudan karşılıklı ters fonksiyonlar kavramını tanıtalım.

Tanım 3

Tanım 2 çerçevesinde $f(x)$ ve $f^(-1)\left(y\right)$ fonksiyonlarına karşılıklı ters fonksiyonlar adı verilir.

Karşılıklı ters fonksiyonların özellikleri

$y=f(x)$ ve $x=g(y)$ fonksiyonlarının karşılıklı olarak tersi olsun, o zaman

$y=f(g\left(y\right))$ ve $x=g(f(x))$

$y=f(x)$ fonksiyonunun tanım alanı, $\ x=g(y)$ fonksiyonunun değer alanına eşittir. Ve $x=g(y)$ fonksiyonunun tanım alanı, $\ y=f(x)$ fonksiyonunun değer alanına eşittir.

$y=f(x)$ ve $x=g(y)$ fonksiyonlarının grafikleri $y=x$ düz çizgisine göre simetriktir.

Fonksiyonlardan biri artarsa ​​(azalırsa), diğer fonksiyon artar (azalır).

Ters Fonksiyonu Bulma

$y=f(x)$ denklemi $x$ değişkenine göre çözülür.

Elde edilen köklerden $X$ aralığına ait olanlar bulunur.

Bulunan $x$, $y$ sayısıyla eşleştirilir.

Örnek 1

$y=x^2$ fonksiyonunun $X=[-1,0]$ aralığında ters fonksiyonunu bulun

Bu fonksiyon $X$ aralığında azalan ve sürekli olduğundan, o zaman $Y=$ aralığında da azalan ve bu aralıkta süreklidir (Teorem 1).

$x$'ı hesaplayalım:

\ \

Uygun $x$'ı seçin:

Cevap: ters fonksiyon $y=-\sqrt(x)$.

Ters fonksiyonları bulma problemleri

Bu bölümde bazı temel fonksiyonlar için ters fonksiyonları ele alacağız. Sorunları yukarıda verilen şemaya göre çözeceğiz.

Örnek 2

$y=x+4$ fonksiyonu için ters fonksiyonu bulun

$y=x+4$ denkleminden $x$'ı bulalım:

Örnek 3

$y=x^3$ fonksiyonu için ters fonksiyonu bulun

Çözüm.

Fonksiyon tüm tanım bölgesi boyunca artan ve sürekli olduğundan, Teorem 1'e göre üzerinde ters sürekli ve artan bir fonksiyon vardır.

$y=x^3$ denkleminden $x$'ı bulalım:

$x$'ın uygun değerlerini bulma

Değer bizim durumumuza uygundur (çünkü tanımın alanı tüm sayılardır)

Değişkenleri yeniden tanımlayalım, ters fonksiyonun şu şekilde olduğunu elde edelim:

Örnek 4

$$ aralığında $y=cosx$ fonksiyonunun ters fonksiyonunu bulun

Çözüm.

$X=\left$ kümesinde $y=cosx$ fonksiyonunu düşünün. $X$ kümesinde süreklidir ve azalmaktadır ve $X=\left$ kümesini $Y=[-1,1]$ kümesine eşler, dolayısıyla ters sürekli monoton fonksiyonun varlığına ilişkin teoreme göre, $y=cosx$ fonksiyonu $ Y$ kümesinde bir ters fonksiyon vardır, bu da $Y=[-1,1]$ kümesinde sürekli ve artandır ve $[-1,1]$ kümesini eşler $\left$ kümesine.

$y=cosx$ denkleminden $x$'yi bulalım:

$x$'ın uygun değerlerini bulma

Değişkenleri yeniden tanımlayalım, ters fonksiyonun şu şekilde olduğunu elde edelim:

Örnek 5

$y=tgx$ fonksiyonunun $\left(-\frac(\pi )(2),\frac(\pi )(2)\right)$ aralığında ters fonksiyonunu bulun.

Çözüm.

$X=\left(-\frac(\pi )(2),\frac(\pi )(2)\right)$ kümesindeki $y=tgx$ fonksiyonunu düşünün. $X$ kümesinde süreklidir ve artmaktadır ve $X=\left(-\frac(\pi )(2),\frac(\pi )(2)\right)$ kümesini $Y kümesine eşler =R$, bu nedenle, ters sürekli monoton fonksiyonun varlığına ilişkin teoreme göre, $Y$ kümesindeki $y=tgx$ işlevi, $Y$ kümesinde de sürekli ve artan bir ters fonksiyona sahiptir. $ ve $R$ kümesini $\left(- \frac(\pi )(2),\frac(\pi )(2)\right)$ kümesine eşler

$y=tgx$ denkleminden $x$'yi bulalım:

$x$'ın uygun değerlerini bulma

Değişkenleri yeniden tanımlayalım, ters fonksiyonun şu şekilde olduğunu elde edelim:

Bir y=f(x) fonksiyonu olsun, X onun tanım bölgesidir, Y ise değer aralığıdır. Her x 0 'nın tek bir y 0 =f(x 0), y 0 Y değerine karşılık geldiğini biliyoruz.

Her y'nin (veya onun  1 parçasının) aynı zamanda X'ten gelen tek bir x'e karşılık geldiği ortaya çıkabilir.

Daha sonra  bölgesinde (veya   kısmında) x=y fonksiyonunun y=f(x) fonksiyonunun ters fonksiyonu olarak tanımlandığını söylüyorlar.

Örneğin:




X =(); Y=)