Dik açıdan çizilmiş yükseklik formülü. Sağ üçgen

Aslında her şey o kadar da korkutucu değil. Elbette yazıda sinüs, kosinüs, tanjant ve kotanjantın “gerçek” tanımına da bakmak gerekir. Ama gerçekten istemiyorum, değil mi? Sevinebiliriz: Bir dik üçgenle ilgili problemleri çözmek için aşağıdaki basit şeyleri doldurmanız yeterlidir:

Peki ya açı? Köşenin karşısında bir bacak var mı, yani karşıt (bir açı için) bacak var mı? Elbette var! Bu bir bacak!

Peki ya açı? Dikkatli bak. Hangi bacak köşeye bitişik? Tabii ki bacak. Bu, bacağın bitişik olduğu açı için ve

Şimdi dikkat edin! Bakın elimizde ne var:

Ne kadar havalı olduğunu görün:

Şimdi teğet ve kotanjanta geçelim.

Şimdi bunu kelimelerle nasıl yazabilirim? Açıya göre bacak nedir? Elbette karşısında - köşenin karşısında "yalan söylüyor". Peki ya bacak? Köşeye bitişik. Peki elimizde ne var?

Pay ve paydanın nasıl yer değiştirdiğini gördünüz mü?

Ve şimdi yine kornerler ve takas yapıldı:

Özet

Öğrendiğimiz her şeyi kısaca yazalım.

Pisagor teoremi:

Dik üçgenlerle ilgili ana teorem Pisagor teoremidir.

Pisagor teoremi

Bu arada, bacakların ve hipotenüsün ne olduğunu iyi hatırlıyor musun? Çok iyi değilse resme bakın - bilginizi tazeleyin

Pisagor teoremini birçok kez kullanmış olmanız oldukça olası, ancak böyle bir teoremin neden doğru olduğunu hiç merak ettiniz mi? Bunu nasıl kanıtlayabilirim? Antik Yunanlılar gibi yapalım. Kenarı olan bir kare çizelim.

Kenarlarını ne kadar akıllıca uzunluklara ayırdığımızı görün ve!

Şimdi işaretli noktaları birleştirelim

Ancak burada başka bir şeye dikkat çektik, ancak siz çizime bakıp bunun neden böyle olduğunu düşünüyorsunuz.

Büyük karenin alanı nedir?

Sağ, .

Daha küçük bir alana ne dersiniz?

Kesinlikle, .

Dört köşenin toplam alanı kalır. Bunları ikişer ikişer alıp hipotenüsleriyle birbirlerine yasladığımızı hayal edin.

Ne oldu? İki dikdörtgen. Bu, "kesiklerin" alanının eşit olduğu anlamına gelir.

Şimdi hepsini bir araya getirelim.

Haydi dönüştürelim:

Böylece Pisagor'u ziyaret ettik; onun teoremini eski bir yöntemle kanıtladık.

Dik üçgen ve trigonometri

Bir dik üçgen için aşağıdaki ilişkiler geçerlidir:

Bir dar açının sinüsü karşı kenarın hipotenüse oranına eşittir

Bir dar açının kosinüsü, komşu kenarın hipotenüse oranına eşittir.

Bir dar açının tanjantı karşı kenarın komşu kenara oranına eşittir.

Bir dar açının kotanjantı, komşu kenarın karşı kenara oranına eşittir.

Ve bir kez daha tüm bunlar bir tablet biçiminde:

Çok rahat!

Dik üçgenlerin eşitliğinin işaretleri

I. İki tarafta

II. Bacak ve hipotenüse göre

III. Hipotenüs ve dar açıya göre

IV. Bacak boyunca ve dar açı

A)

B)

Dikkat! Burada bacakların “uygun” olması çok önemlidir. Örneğin, eğer şu şekilde giderse:

O halde ÜÇGENLER EŞİT DEĞİLDİR aynı dar açıya sahip olmalarına rağmen.

Gerekiyor her iki üçgende de bacak bitişikti veya her ikisinde de zıttı.

Dik üçgenlerin eşitlik işaretlerinin, üçgenlerin eşitlik işaretlerinden ne kadar farklı olduğunu fark ettiniz mi?

Konuya bir göz atın ve “sıradan” üçgenlerin eşitliği için elemanlarından üçünün eşit olması gerektiğine dikkat edin: iki kenar ve aralarındaki açı, iki açı ve aralarındaki kenar veya üç kenar.

Ancak dik üçgenlerin eşitliği için yalnızca karşılık gelen iki öğe yeterlidir. Harika, değil mi?

Dik üçgenlerin benzerlik işaretleri ile durum yaklaşık olarak aynıdır.

Dik üçgenlerin benzerlik belirtileri

I. Dar bir açı boyunca

II. İki tarafta

III. Bacak ve hipotenüse göre

Dik üçgende medyan

Bu neden böyle?

Dik üçgen yerine tam bir dikdörtgen düşünün.

Bir köşegen çizelim ve bir nokta düşünelim; köşegenlerin kesişme noktası. Dikdörtgenin köşegenleri hakkında ne biliyorsunuz?

Peki bundan ne sonuç çıkıyor?

Böylece ortaya çıktı

1. - medyan:

Bu gerçeği unutmayın! Çok yardımcı oluyor!

Daha da şaşırtıcı olan ise bunun tam tersinin de geçerli olmasıdır.

Hipotenüse çizilen medyanın hipotenüsün yarısına eşit olmasından ne gibi bir fayda elde edilebilir? Hadi resme bakalım

Dikkatli bak. Elimizde: , yani noktadan üçgenin üç köşesine olan mesafelerin eşit olduğu ortaya çıktı. Ancak üçgende üçgenin üç köşesine de mesafeleri eşit olan tek bir nokta vardır ve bu da ÇEMBERİN MERKEZİdir. Peki ne oldu?

O halde şu "ayrıca..." ile başlayalım.

Şimdi ve'ye bakalım.

Ancak benzer üçgenlerin tüm açıları eşittir!

Aynı şey hakkında da söylenebilir ve

Şimdi birlikte çizelim:

Bu “üçlü” benzerlikten ne gibi faydalar elde edilebilir?

Mesela - Dik üçgenin yüksekliği için iki formül.

İlgili tarafların ilişkilerini yazalım:

Yüksekliği bulmak için orantıyı çözeriz ve şunu elde ederiz: ilk formül "Dik üçgende yükseklik":

Artık bu bilgiyi uygulayarak ve başkalarıyla birleştirerek, dik üçgenle ilgili her türlü sorunu çözeceksiniz!

O halde benzerliği uygulayalım: .

Ne olacak şimdi?

Yine orantıyı çözüyoruz ve ikinci formülü elde ediyoruz:

Bu formüllerin ikisini de çok iyi hatırlamanız ve size hangisi daha uygunsa onu kullanmanız gerekiyor.

Tekrar yazalım

Pisagor teoremi:

Bir dik üçgende hipotenüsün karesi, dik kenarların karelerinin toplamına eşittir: .

Dik üçgenlerin eşitliğinin işaretleri:

• iki tarafta:
• bacak ve hipotenüse göre: veya
• bacak boyunca ve bitişik dar açı boyunca: veya
• bacak boyunca ve karşıt dar açıda: veya
• hipotenüs ve dar açıya göre: veya.

Dik üçgenlerin benzerlik işaretleri:

• bir akut köşe: veya
• iki bacağın orantılılığından:
• bacağın ve hipotenüsün orantılılığından: veya.

Bir dik üçgende sinüs, kosinüs, teğet, kotanjant

• Bir dik üçgenin dar açısının sinüsü, karşı tarafın hipotenüse oranıdır:
• Bir dik üçgenin dar açısının kosinüsü, bitişik kenarın hipotenüse oranıdır:
• Bir dik üçgenin dar açısının tanjantı, karşı tarafın bitişik kenara oranıdır:
• Bir dik üçgenin dar açısının kotanjantı, komşu kenarın karşı kenara oranıdır: .

Bir dik üçgenin yüksekliği: veya.

Bir dik üçgende dik açının tepe noktasından çizilen kenarortay hipotenüsün yarısına eşittir: .

Dik üçgenin alanı:

• bacaklar yoluyla:

Üçgenler.

Temel konseptler.

Üçgen aynı doğru üzerinde yer almayan üç parça ve üç noktadan oluşan şekildir.

Segmentler denir partiler ve noktalar zirveler.

Açıların toplamıüçgen 180°'dir.

Üçgenin yüksekliği.

Üçgen yüksekliği- bu, tepe noktasından karşı tarafa çizilen bir diktir.

Dar bir üçgende yükseklik üçgenin içinde bulunur (Şekil 1).

Bir dik üçgende bacaklar üçgenin yükseklikleridir (Şekil 2).

Geniş açılı bir üçgende yükseklik üçgenin dışına uzanır (Şekil 3).

Bir üçgenin yüksekliğinin özellikleri:

Bir üçgenin ortaortayı.

Bir üçgenin açıortayı- bu, tepe noktasının köşesini ikiye bölen ve tepe noktasını karşı taraftaki bir noktaya bağlayan bir segmenttir (Şekil 5).

Ortayörün özellikleri:

Bir üçgenin medyanı.

Bir üçgenin medyanı- bu, tepe noktasını karşı tarafın ortasına bağlayan bir segmenttir (Şekil 9a).

Medyanın uzunluğu aşağıdaki formül kullanılarak hesaplanabilir: 2B 2 + 2C 2 - A 2 anne 2 = —————— 4 Nerede anne- orta refüj yana çekilmiş A. Bir dik üçgende hipotenüse çizilen kenarortay hipotenüsün yarısına eşittir: C m c = — 2 Nerede m c- hipotenüse çizilen medyan C(Şekil 9c) Üçgenin kenarortayları bir noktada (üçgenin kütle merkezinde) kesişir ve tepe noktasından itibaren sayılarak 2:1 oranında bu noktaya bölünür. Yani üçgenin tepe noktasından merkeze doğru olan kısmı, merkezden yanlara doğru olan kısımdan iki kat daha büyüktür (Şekil 9c). Bir üçgenin üç medyanı onu altı eşit üçgene böler.

Üçgenin orta çizgisi.

Üçgenin orta çizgisi- bu, iki tarafının orta noktalarını birleştiren bir segmenttir (Şekil 10).

Üçgenin orta çizgisi üçüncü kenara paralel ve yarısına eşittir

Bir üçgenin dış açısı.

Dış köşe Bir üçgenin açısı, bitişik olmayan iki iç açının toplamına eşittir (Şekil 11).

Bir üçgenin bir dış açısı, komşu olmayan herhangi bir açıdan daha büyüktür.

Sağ üçgen.

Sağ üçgen dik açılı bir üçgendir (Şek. 12).

Bir dik üçgenin dik açının karşısındaki kenarına denir hipotenüs.

Diğer iki tarafa denir bacaklar.

Dik üçgende orantılı bölümler.

1) Bir dik üçgende dik açıdan çizilen yükseklik üç benzer üçgen oluşturur: ABC, ACH ve HCB (Şekil 14a). Buna göre yüksekliğin oluşturduğu açılar A ve B açılarına eşittir.

Şekil 14a

İkizkenar üçgen.

İkizkenar üçgen iki tarafı eşit olan bir üçgendir (Şek. 13).

Bu eşit kenarlara denir taraflar ve üçüncüsü - temelüçgen.

İkizkenar üçgende taban açıları eşittir. (Üçgenimizde A açısı C açısına eşittir).

Bir ikizkenar üçgende tabana çizilen kenarortay üçgenin hem açıortayı hem de yüksekliğidir.

Eşkenar üçgen.

Eşkenar üçgen, tüm kenarların eşit olduğu bir üçgendir (Şekil 14).

Eşkenar üçgenin özellikleri:

Üçgenlerin dikkat çekici özellikleri.

Üçgenler, bu şekilleri içeren problemleri başarıyla çözmenize yardımcı olacak benzersiz özelliklere sahiptir. Bu özelliklerden bazıları yukarıda özetlenmiştir. Ancak bunları birkaç harika özellik daha ekleyerek tekrarlıyoruz:

1) Açıları 90°, 30° ve 60° olan bir dik üçgende B 30°'lik bir açının karşısında yer alan şuna eşittir: hipotenüsün yarısı. BacakA daha fazla bacakB√3 kez (Şek. 15 A). Örneğin, b kenarı 5 ise hipotenüs C zorunlu olarak 10'a eşittir ve bacak A 5√3'e eşittir. 2) Açıları 90°, 45° ve 45° olan bir dik ikizkenar üçgende hipotenüs kenardan √2 kat daha büyüktür (Şekil 15). B). Örneğin, eğer kenarlar 5 ise hipotenüs 5√2 olur. 3) Üçgenin orta çizgisi paralel kenarın yarısına eşittir (Şek. 15) İle). Örneğin bir üçgenin bir kenarı 10 ise ona paralel olan orta çizgi 5 olur. 4) Bir dik üçgende hipotenüse çizilen kenarortay hipotenüsün yarısına eşittir (Şekil 9c): m c= a/2. 5) Bir üçgenin bir noktada kesişen kenarortayları bu noktaya 2:1 oranında bölünür. Yani, tepe noktasından kenarortayların kesişme noktasına kadar olan bölüm, kenarortayların kesişme noktasından üçgenin kenarına kadar olan bölümün iki katı kadar büyüktür (Şekil 9c). 6) Bir dik üçgende hipotenüsün ortası çevrel çemberin merkezidir (Şek. 15) D).

Üçgenlerin eşitliğinin işaretleri.

Eşitliğin ilk işareti: Bir üçgenin iki kenarı ve aralarındaki açı başka bir üçgenin iki kenarına ve aralarındaki açıya eşitse bu üçgenler eştir.

Eşitliğin ikinci işareti: Bir üçgenin bir kenarı ve ona komşu açılar başka bir üçgenin kenarına ve komşu açılarına eşitse bu üçgenler eştir.

Eşitliğin üçüncü işareti: Bir üçgenin üç kenarı başka bir üçgenin üç kenarına eşitse bu üçgenler eştir.

Üçgen eşitsizliği.

Herhangi bir üçgende her bir kenar diğer iki kenarın toplamından küçüktür.

Pisagor teoremi.

Bir dik üçgende hipotenüsün karesi, dik kenarların karelerinin toplamına eşittir:

C 2 = A 2 + B 2 .

Bir üçgenin alanı.

1) Bir üçgenin alanı, kenarının ve bu kenara çizilen yüksekliğin çarpımının yarısına eşittir:

Ah
S = ——
2

2) Bir üçgenin alanı, herhangi iki tarafının çarpımının yarısına ve aralarındaki açının sinüsüne eşittir:

1
S = — AB · AC. · günah A
2

Bir daire etrafında çevrelenmiş bir üçgen.

Tüm kenarlarına değiyorsa, üçgen içine yazılmış bir daireye denir (Şek. 16). A).

Bir daire içine yazılmış bir üçgen.

Bir üçgenin tüm köşeleriyle ona değmesi durumunda bir dairenin içine yazıldığı söylenir (Şekil 17). A).

Bir dik üçgenin dar açısının sinüs, kosinüs, teğet, kotanjantı (Şekil 18).

Sinüs dar açı X zıt Bacaktan hipotenüse.
Şu şekilde ifade edilir: günahX.

Kosinüs dar açı X bir dik üçgenin oranı bitişik Bacaktan hipotenüse.
Aşağıdaki şekilde gösterilir: çünkü X.

Teğet dar açı X- bu, karşı tarafın bitişik tarafa oranıdır.
Aşağıdaki şekilde belirlenmiştir: tgX.

Kotanjant dar açı X- bu, bitişik tarafın karşı tarafa oranıdır.
Aşağıdaki şekilde belirlenmiştir: ctgX.

Tüzük:

Bacak köşenin karşısında X, hipotenüs ile günahın çarpımına eşittir X:

b = c günah X

Bacak köşeye bitişik X, hipotenüs ve cos çarpımına eşittir X:

a = cçünkü X

Bacak köşenin karşısında X, ikinci ayağın tg çarpımına eşittir X:

b = bir tg X

Bacak köşeye bitişik X, ikinci ayağın ctg çarpımına eşittir X:

a = b· ctg X.

Herhangi bir dar açı için X:

günah (90° - X) = çünkü X

çünkü (90° - X) = günah X

Sağ üçgen- bu, açılardan birinin düz, yani 90 dereceye eşit olduğu bir üçgendir.

• Dik açının karşısındaki kenara hipotenüs adı verilir (şekilde gösterilen şekilde) C veya AB)
• Dik açıya bitişik olan tarafa bacak denir. Her dik üçgenin iki bacağı vardır (şekilde bunlar şu şekilde gösterilmiştir: A ve b veya AC ve BC)

Dik üçgenin formülleri ve özellikleri

Formül tanımları:

(yukarıdaki resme bakınız)

a, b- bir dik üçgenin bacakları

C- hipotenüs

α, β - bir üçgenin dar açıları

S- kare

H- dik açının tepesinden hipotenüse kadar indirilen yükseklik

anne A karşı köşeden ( α )

m b- orta refüj yana çekilmiş B karşı köşeden ( β )

m c- orta refüj yana çekilmiş C karşı köşeden ( γ )

İÇİNDE dik üçgen bacaklardan herhangi biri hipotenüsten küçükse(Formül 1 ve 2). Bu özellik Pisagor teoreminin bir sonucudur.

Herhangi bir akut açının kosinüsü birden az (Formül 3 ve 4). Bu özellik öncekinin devamıdır. Bacakların herhangi biri hipotenüsten küçük olduğundan, bacağın hipotenüse oranı her zaman birden küçüktür.

Hipotenüsün karesi bacakların karelerinin toplamına eşittir (Pisagor teoremi). (Formül 5). Bu özellik problem çözerken sürekli olarak kullanılır.

Dik üçgenin alanı bacakların çarpımının yarısına eşit (Formül 6)

Kare medyanların toplamı bacaklara eşittir, ortancanın hipotenüsün beş karesine ve hipotenüsün beş karesinin dörde bölünmesine eşittir (Formül 7). Yukarıdakilere ek olarak, 5 formül daha bu nedenle medyanın özelliklerini daha ayrıntılı olarak anlatan “Dik Üçgenin Medyanı” dersini de okumanız önerilir.

Yükseklik Bir dik üçgenin uzunluğu, bacakların çarpımının hipotenüse bölünmesine eşittir (Formül 8)

Bacakların kareleri, hipotenüse indirilen yüksekliğin karesiyle ters orantılıdır (Formül 9). Bu özdeşlik aynı zamanda Pisagor teoreminin sonuçlarından biridir.

Hipotenüs uzunluğuçevrelenen dairenin çapına (iki yarıçap) eşittir (Formül 10). Bir dik üçgenin hipotenüsü çevrel çemberin çapıdır. Bu özellik genellikle problem çözmede kullanılır.

Yazılı yarıçap V dik üçgen daire Bu üçgenin bacaklarının toplamından hipotenüsün uzunluğunun çıkarılmasıyla elde edilen ifadenin yarısı kadar bulunabilir. Veya bacakların çarpımının belirli bir üçgenin tüm kenarlarının (çevresinin) toplamına bölünmesiyle elde edilir. (Formül 11)
Açının sinüsü tam tersiyle ilişki bu açı Bacaktan hipotenüse(sinüs tanımı gereği). (Formül 12). Bu özellik problem çözerken kullanılır. Kenarların boyutlarını bilerek oluşturdukları açıyı bulabilirsiniz.

Bir dik üçgende A açısının (α, alfa) kosinüsü şuna eşit olacaktır: davranış bitişik bu açı Bacaktan hipotenüse(sinüs tanımı gereği). (Formül 13)

Mülkiyet: 1. Herhangi bir dik üçgende, dik açıdan (hipotenüs tarafından) alınan yükseklik, dik üçgeni üç benzer üçgene böler.

Mülkiyet: 2. Hipotenüse indirilen dik üçgenin yüksekliği, bacakların hipotenüs üzerindeki çıkıntılarının geometrik ortalamasına (veya yüksekliğin hipotenüsü böldüğü bölümlerin geometrik ortalamasına) eşittir.

Mülkiyet: 3. Bacak, hipotenüsün geometrik ortalamasına ve bu bacağın hipotenüse izdüşümüne eşittir.

Mülkiyet: 4. 30 derecelik bir açının karşısındaki kenar hipotenüsün yarısına eşittir.

Formül 1.

Formül 2., hipotenüs nerede; , bacaklar.

Mülkiyet: 5. Bir dik üçgende hipotenüse çizilen kenarortay bunun yarısına ve çevrelenen dairenin yarıçapına eşittir.

Özellik: 6. Bir dik üçgenin kenarları ve açıları arasındaki ilişki:

44. Kosinüs teoremi. Sonuçlar: paralelkenarın köşegenleri ve kenarları arasındaki ilişki; üçgenin tipinin belirlenmesi; bir üçgenin medyanının uzunluğunu hesaplamak için formül; Bir üçgen açının kosinüsünün hesaplanması.

İş bitimi -

Bu konu şu bölüme aittir:

Sınıf. Temel planimetri üzerine konferans programı

Komşu açıların özelliği.. Bir kenarları ortak olan ve diğer ikisi düz bir çizgi oluşturan iki açının komşu olması tanımı..

Bu konuyla ilgili ek materyale ihtiyacınız varsa veya aradığınızı bulamadıysanız, çalışma veritabanımızdaki aramayı kullanmanızı öneririz:

Alınan materyalle ne yapacağız:

Bu materyal sizin için yararlı olduysa, onu sosyal ağlardaki sayfanıza kaydedebilirsiniz:

Geometrik problemleri çözerken böyle bir algoritmayı takip etmek faydalıdır. Sorunun koşullarını okurken gerekli

• Çizim yapmak. Çizim, sorunun koşullarına mümkün olduğunca uygun olmalıdır, bu nedenle asıl görevi çözümü bulmaya yardımcı olmaktır.
• Sorun ifadesindeki tüm verileri çizime koyun
• Problemde ortaya çıkan tüm geometrik kavramları yazın
• Bu kavramlarla ilgili tüm teoremleri hatırlayın
• Bu teoremlerden çıkan geometrik bir şeklin elemanları arasındaki tüm ilişkileri çizim üzerine çizin

Örneğin, problem bir üçgenin açısının açıortay kelimelerini içeriyorsa, bir açıortayın tanımını ve özelliklerini hatırlamanız ve çizimde eşit veya orantılı parçaları ve açıları belirtmeniz gerekir.

Bu makalede, problemleri başarılı bir şekilde çözmek için bilmeniz gereken bir üçgenin temel özelliklerini bulacaksınız.

ÜÇGEN.

Bir üçgenin alanı.

1. ,

burada - üçgenin keyfi bir tarafı - bu tarafa indirilen yükseklik.

2. ,

burada ve üçgenin keyfi kenarlarıdır ve bu kenarlar arasındaki açıdır:

3. Heron'un formülü:

İşte üçgenin kenar uzunlukları, üçgenin yarı çevresi,

4. ,

burada üçgenin yarı çevresi ve yazılı dairenin yarıçapı var.

Teğet doğru parçalarının uzunlukları olsun.

O zaman Heron'un formülü şu şekilde yazılabilir:

6. ,

burada - üçgenin kenarlarının uzunlukları - çevrelenen dairenin yarıçapı.

Bir üçgenin bu kenarı m:n oranında bölen tarafında bir nokta alınırsa, bu noktayı karşı açının tepe noktasına birleştiren doğru parçası, üçgeni alanları orantılı iki üçgene böler. m: n:

Benzer üçgenlerin alanlarının oranı benzerlik katsayısının karesine eşittir.

Bir üçgenin medyanı

Bu, bir üçgenin tepe noktasını karşı kenarın ortasına bağlayan bir segmenttir.

Bir üçgenin medyanları bir noktada kesişir ve tepe noktasından itibaren sayılarak 2:1 oranında kesişme noktasına bölünür.

Normal bir üçgenin kenarortaylarının kesişme noktası, ortancayı iki parçaya böler; bunlardan küçüğü yazılı dairenin yarıçapına eşittir ve büyüğü ise çevrelenen dairenin yarıçapına eşittir.

Sınırlandırılmış dairenin yarıçapı, yazılı dairenin yarıçapının iki katıdır: R=2r

Medyan uzunluk keyfi üçgen

,

burada - kenara çizilen medyan - üçgenin kenarlarının uzunlukları.

Bir üçgenin açıortayı

Bu, bir üçgenin herhangi bir açısının, bu açının tepe noktasını karşı kenarla birleştiren açıortay kısmıdır.

Bir üçgenin açıortayı bir tarafı bitişik kenarlarla orantılı parçalara böler:

Bir üçgenin açıortayları yazılı dairenin merkezi olan bir noktada kesişir.

Açıortayın tüm noktaları açının kenarlarından eşit uzaklıktadır.

Üçgen yüksekliği

Bu, üçgenin tepe noktasından karşı tarafa bırakılan dik bir bölüm veya onun devamıdır. Geniş açılı bir üçgende dar açının tepe noktasından çizilen yükseklik üçgenin dışındadır.

Bir üçgenin yükseklikleri bir noktada kesişir, buna denir üçgenin diklik merkezi.

Bir üçgenin yüksekliğini bulmak için yana doğru çizildiğinde, alanını herhangi bir şekilde bulmanız ve ardından formülü kullanmanız gerekir:

Bir üçgenin çevrel çemberinin merkezi, üçgenin kenarlarına çizilen dik açıortayların kesişme noktasında yer alır.

Bir üçgenin çevre yarıçapı aşağıdaki formüller kullanılarak bulunabilir:

İşte üçgenin kenar uzunlukları ve üçgenin alanı.

,

üçgenin kenar uzunluğu nerede ve karşı açıdır. (Bu formül sinüs teoreminden gelir.)

Üçgen eşitsizliği

Üçgenin her bir kenarı diğer ikisinin toplamından küçük ve farkından büyüktür.

Herhangi iki kenarın uzunluklarının toplamı her zaman üçüncü kenarın uzunluğundan daha büyüktür:

Büyük tarafın karşısında daha büyük açı yer alır; Büyük açının karşısında büyük kenar yer alır:

Eğer öyleyse, o zaman tam tersi.

Sinüs teoremi:

Bir üçgenin kenarları karşıt açıların sinüsleriyle orantılıdır:

Kosinüs teoremi:

Bir üçgenin bir kenarının karesi, diğer iki kenarın karelerinin toplamına, bu kenarların çarpımının iki katı ile aralarındaki açının kosinüsü olmadan eşittir:

Sağ üçgen

- Bu, açılarından biri 90° olan bir üçgendir.

Bir dik üçgenin dar açılarının toplamı 90°'dir.

Hipotenüs 90° açının karşısındaki kenardır. Hipotenüs en uzun kenardır.

Pisagor teoremi:

hipotenüsün karesi bacakların karelerinin toplamına eşittir:

Bir dik üçgenin içine yazılan dairenin yarıçapı eşittir

,

burada yazılı dairenin yarıçapı, - bacaklar, - hipotenüs:

Bir dik üçgenin çevrel çemberinin merkezi hipotenüsün ortasında yer alır:

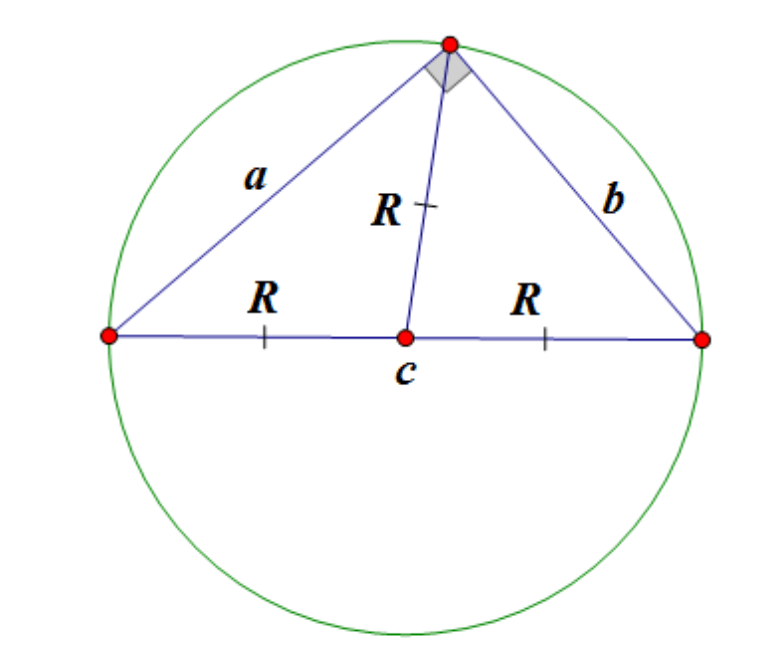
Hipotenüse çizilen bir dik üçgenin medyanı, hipotenüsün yarısına eşittir.

Dik üçgenin sinüs, kosinüs, tanjant ve kotanjantının tanımı Bakmak

Dik üçgendeki elemanların oranı:

Bir dik açının tepe noktasından çizilen bir dik üçgenin yüksekliğinin karesi, bacakların hipotenüse izdüşümlerinin çarpımına eşittir:

Bacağın karesi, hipotenüsün çarpımına ve bacağın hipotenüse izdüşümüne eşittir:

Bacak köşenin karşısında yatıyor hipotenüsün yarısına eşit:

İkizkenar üçgen.

Tabana çizilen ikizkenar üçgenin açıortayı kenarortay ve yüksekliktir.

İkizkenar üçgende taban açıları eşittir.

Tepe açısı.

Ve - taraflar,

Ve - tabandaki açılar.

Yükseklik, açıortay ve ortanca.

Dikkat! Yan tarafa çizilen yükseklik, açıortay ve orta refüj çakışmıyor.

Düzenli üçgen

(veya eşkenar üçgen ) tüm kenarları ve açıları birbirine eşit olan bir üçgendir.

Düzenli bir üçgenin alanı eşittir

üçgenin kenar uzunluğu nerede.

Düzenli bir üçgenin içine yazılmış bir dairenin merkezi, düzgün bir üçgen etrafında çevrelenen dairenin merkezi ile çakışır ve kenarortayların kesişme noktasında yer alır.

Düzgün bir üçgenin kenarortaylarının kesişme noktası ortancayı iki parçaya böler; bunlardan küçüğü yazılı dairenin yarıçapına eşittir ve büyüğü ise çevrelenen dairenin yarıçapına eşittir.

Bir ikizkenar üçgenin açılarından biri 60° ise bu üçgen düzgün üçgendir.

Üçgenin orta çizgisi

Bu, iki tarafın orta noktalarını birleştiren bir segmenttir.

Şekilde DE ABC üçgeninin orta çizgisidir.

Üçgenin orta çizgisi üçüncü kenara paralel ve yarısına eşittir: DE||AC, AC=2DE

Bir üçgenin dış açısı

Bu, üçgenin herhangi bir açısına komşu olan açıdır.

Bir üçgenin bir dış açısı, kendisine komşu olmayan iki açının toplamına eşittir.

Dış açı trigonometrik fonksiyonlar:

Üçgenlerin eşitliğinin işaretleri:

1 . Bir üçgenin iki kenarı ve aralarındaki açı, başka bir üçgenin sırasıyla iki kenarına ve aralarındaki açıya eşitse, bu tür üçgenler eştir.

2 . Bir üçgenin bir kenarı ve komşu iki açısı, başka bir üçgenin bir kenarı ve komşu iki açısına sırasıyla eşitse, bu tür üçgenler eştir.

3 Bir üçgenin üç kenarı sırasıyla başka bir üçgenin üç kenarına eşitse bu üçgenler eştir.

Önemli: Bir dik üçgende iki açı açıkça eşit olduğundan, o zaman iki dik üçgenin eşitliği yalnızca iki unsurun eşitliği gereklidir: iki kenar veya bir kenar ve bir dar açı.

Üçgenlerin benzerlik belirtileri:

1 . Bir üçgenin iki kenarı diğer üçgenin iki kenarıyla orantılıysa ve bu kenarlar arasındaki açılar eşitse bu üçgenler benzerdir.

2 . Bir üçgenin üç kenarı başka bir üçgenin üç kenarıyla orantılıysa bu üçgenler benzerdir.

3 . Bir üçgenin iki açısı diğer üçgenin iki açısına eşitse bu üçgenler benzerdir.

Önemli: Benzer üçgenlerde benzer kenarlar eşit açıların karşısında yer alır.

Menelaus'un teoremi

Bir doğrunun bir üçgenle kesişmesine izin verin ve bu onun yan ile kesişme noktası, yan ile kesişme noktası ve yan'ın devamı ile kesişme noktası olsun. Daha sonra