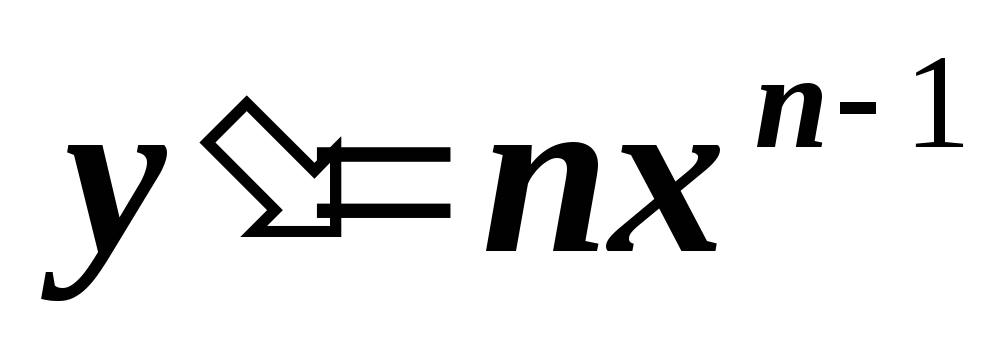Logarithm value. Logarithmic Expressions
Maintaining your privacy is important to us. For this reason, we have developed a Privacy Policy that describes how we use and store your information. Please review our privacy practices and let us know if you have any questions.
Collection and use of personal information
Personal information refers to data that can be used to identify certain person or connection with him.
You may be asked to provide your personal information at any time when you contact us.
Below are some examples of the types of personal information we may collect and how we may use such information.
What personal information do we collect:
- When you submit an application on the site, we may collect various information, including your name, telephone number, address Email etc.
How we use your personal information:
- Collected by us personal information allows us to contact you and inform you about unique offers, promotions and other events and upcoming events.
- From time to time, we may use your personal information to send important notices and communications.
- We may also use personal information for internal purposes such as auditing, data analysis and various studies in order to improve the services we provide and provide you with recommendations regarding our services.
- If you participate in a prize draw, contest or similar promotion, we may use the information you provide to administer such programs.
Disclosure of information to third parties
We do not disclose the information received from you to third parties.
Exceptions:
- If necessary, in accordance with the law, judicial procedure, in legal proceedings, and/or on the basis of public requests or requests from government agencies in the Russian Federation - to disclose your personal information. We may also disclose information about you if we determine that such disclosure is necessary or appropriate for security, law enforcement, or other public importance purposes.
- In the event of a reorganization, merger, or sale, we may transfer the personal information we collect to the applicable successor third party.
Protection of personal information
We take precautions - including administrative, technical and physical - to protect your personal information from loss, theft, and misuse, as well as unauthorized access, disclosure, alteration and destruction.
Respecting your privacy at the company level
To ensure that your personal information is secure, we communicate privacy and security standards to our employees and strictly enforce privacy practices.
The focus of this article is logarithm. Here we will give a definition of a logarithm, show the accepted notation, give examples of logarithms, and talk about natural and decimal logarithms. After that, let's look at the main logarithmic identity.
Page navigation.
Definition of logarithm
The concept of a logarithm arises when solving a problem in a certain inverse sense, when you need to find an exponent in known value degree and known basis.
But enough prefaces, it’s time to answer the question “what is a logarithm”? Let us give the corresponding definition.
Definition.
Logarithm of b to base a, where a>0, a≠1 and b>0 is the exponent to which you need to raise the number a to get b as a result.
At this stage, we note that the spoken word “logarithm” should immediately raise two follow-up questions: “what number” and “on what basis.” In other words, there is simply no logarithm, but only the logarithm of a number to some base.
Let's enter right away logarithm notation: the logarithm of a number b to base a is usually denoted as log a b. The logarithm of a number b to base e and the logarithm to base 10 have their own special designations lnb and logb, respectively, that is, they write not log e b, but lnb, and not log 10 b, but lgb.
Now we can give: .
And the records 
do not make sense, since in the first of them under the sign of the logarithm there is a negative number, in the second there is a negative number in the base, and in the third there is a negative number under the logarithm sign and a unit in the base.
Now let's talk about rules for reading logarithms. Log a b is read as "the logarithm of b to base a". For example, log 2 3 is the logarithm of three to base 2, and is the logarithm of two point two thirds to base 2 Square root out of five. The logarithm to base e is called natural logarithm, and the notation lnb reads "natural logarithm of b". For example, ln7 is the natural logarithm of seven, and we will read it as the natural logarithm of pi. The base 10 logarithm also has a special name - decimal logarithm, and lgb is read as "decimal logarithm of b". For example, lg1 is the decimal logarithm of one, and lg2.75 is the decimal logarithm of two point seven five hundredths.
It is worth dwelling separately on the conditions a>0, a≠1 and b>0, under which the definition of the logarithm is given. Let us explain where these restrictions come from. An equality of the form called , which directly follows from the definition of logarithm given above, will help us do this.
Let's start with a≠1. Since one to any power is equal to one, the equality can only be true when b=1, but log 1 1 can be any real number. To avoid this ambiguity, a≠1 is assumed.
Let us justify the expediency of the condition a>0. With a=0, by the definition of a logarithm, we would have equality, which is only possible with b=0. But then log 0 0 can be any non-zero real number, since zero to any non-zero power is zero. The condition a≠0 allows us to avoid this ambiguity. And when a<0 нам бы пришлось отказаться от рассмотрения рациональных и иррациональных значений логарифма, так как степень с рациональным и иррациональным показателем определена лишь для неотрицательных оснований. Поэтому и принимается условие a>0 .
Finally, the condition b>0 follows from the inequality a>0, since , and the value of a power with a positive base a is always positive.
To conclude this point, let’s say that the stated definition of the logarithm allows you to immediately indicate the value of the logarithm when the number under the logarithm sign is a certain power of the base. Indeed, the definition of a logarithm allows us to state that if b=a p, then the logarithm of the number b to base a is equal to p. That is, the equality log a a p =p is true. For example, we know that 2 3 =8, then log 2 8=3. We will talk more about this in the article.
Let's start with properties of the logarithm of one. Its formulation is as follows: the logarithm of unity is equal to zero, that is, log a 1=0 for any a>0, a≠1. The proof is not difficult: since a 0 =1 for any a satisfying the above conditions a>0 and a≠1, then the equality log a 1=0 to be proved follows immediately from the definition of the logarithm.
Let us give examples of the application of the considered property: log 3 1=0, log1=0 and .
Let's move on to the next property: the logarithm of a number equal to the base is equal to one, that is, log a a=1 for a>0, a≠1. Indeed, since a 1 =a for any a, then by definition of the logarithm log a a=1.
Examples of using this property of logarithms are the equalities log 5 5=1, log 5.6 5.6 and lne=1.
For example, log 2 2 7 =7, log10 -4 =-4 and 
.
Logarithm of the product of two positive numbers x and y is equal to the product of the logarithms of these numbers: log a (x y)=log a x+log a y, a>0 , a≠1 . Let us prove the property of the logarithm of a product. Due to the properties of the degree a log a x+log a y =a log a x ·a log a y, and since by the main logarithmic identity a log a x =x and a log a y =y, then a log a x ·a log a y =x·y. Thus, a log a x+log a y =x·y, from which, by the definition of a logarithm, the equality being proved follows.
Let's show examples of using the property of the logarithm of a product: log 5 (2 3)=log 5 2+log 5 3 and 
.
The property of the logarithm of a product can be generalized to the product of a finite number n of positive numbers x 1 , x 2 , …, x n as log a (x 1 ·x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n . This equality can be proven without problems.
For example, the natural logarithm of a product can be replaced by the sum of three natural logarithms numbers 4 , e , and .
Logarithm of the quotient of two positive numbers x and y is equal to the difference between the logarithms of these numbers. The property of the logarithm of a quotient corresponds to a formula of the form , where a>0, a≠1, x and y are some positive numbers. The validity of this formula is proven as well as the formula for the logarithm of a product: since 
, then by definition of a logarithm.
Here is an example of using this property of the logarithm: 
.
Let's move on to property of the logarithm of the power. The logarithm of a degree is equal to the product of the exponent and the logarithm of the modulus of the base of this degree. Let us write this property of the logarithm of a power as a formula: log a b p =p·log a |b|, where a>0, a≠1, b and p are numbers such that the degree b p makes sense and b p >0.
First we prove this property for positive b. The basic logarithmic identity allows us to represent the number b as a log a b , then b p =(a log a b) p , and the resulting expression, due to the property of power, is equal to a p·log a b . So we come to the equality b p =a p·log a b, from which, by the definition of a logarithm, we conclude that log a b p =p·log a b.
It remains to prove this property for negative b. Here we note that the expression log a b p for negative b makes sense only for even exponents p (since the value of the degree b p must be greater than zero, otherwise the logarithm will not make sense), and in this case b p =|b| p. Then b p =|b| p =(a log a |b|) p =a p·log a |b|, from where log a b p =p·log a |b| .
For example, 
and ln(-3) 4 =4·ln|-3|=4·ln3 .
It follows from the previous property property of the logarithm from the root: the logarithm of the nth root is equal to the product of the fraction 1/n by the logarithm of the radical expression, that is, 
, where a>0, a≠1, n – natural number, greater than one, b>0.
The proof is based on the equality (see), which is valid for any positive b, and the property of the logarithm of the power: 
.
Here is an example of using this property: 
.
Now let's prove formula for moving to a new logarithm base kind 
. To do this, it is enough to prove the validity of the equality log c b=log a b·log c a. The basic logarithmic identity allows us to represent the number b as a log a b , then log c b=log c a log a b . It remains to use the property of the logarithm of the degree: log c a log a b =log a b log c a. This proves the equality log c b=log a b·log c a, which means that the formula for transition to a new base of the logarithm has also been proven.
Let's show a couple of examples of using this property of logarithms: and 
.
The formula for moving to a new base allows you to move on to working with logarithms that have a “convenient” base. For example, with its help you can switch to natural or decimal logarithms so that you can calculate the value of the logarithm from the table of logarithms. The formula for moving to a new logarithm base also allows, in some cases, to find the value of a given logarithm when the values of some logarithms with other bases are known.
A special case of the formula for transition to a new logarithm base for c=b of the form is often used 
. This shows that log a b and log b a – . Eg, 
.
The formula is also often used 
, which is convenient for finding logarithm values. To confirm our words, we will show how it can be used to calculate the value of a logarithm of the form . We have 
. To prove the formula 
it is enough to use the formula for transition to a new base of the logarithm a: 
.
It remains to prove the properties of comparison of logarithms.
Let us prove that for any positive numbers b 1 and b 2, b 1 log a b 2 , and for a>1 – the inequality log a b 1 Finally, it remains to prove the last of the listed properties of logarithms. Let us limit ourselves to the proof of its first part, that is, we will prove that if a 1 >1, a 2 >1 and a 1 1 is true log a 1 b>log a 2 b . The remaining statements of this property of logarithms are proved according to a similar principle. Let's use the opposite method. Suppose that for a 1 >1, a 2 >1 and a 1 1 is true log a 1 b≤log a 2 b . Based on the properties of logarithms, these inequalities can be rewritten as 
And 
respectively, and from them it follows that log b a 1 ≤log b a 2 and log b a 1 ≥log b a 2, respectively. Then, according to the properties of powers with the same bases, the equalities b log b a 1 ≥b log b a 2 and b log b a 1 ≥b log b a 2 must hold, that is, a 1 ≥a 2 . So we came to a contradiction to the condition a 1
Bibliography.
- Kolmogorov A.N., Abramov A.M., Dudnitsyn Yu.P. and others. Algebra and the beginnings of analysis: Textbook for grades 10 - 11 of general education institutions.
- Gusev V.A., Mordkovich A.G. Mathematics (a manual for those entering technical schools).
Logarithm of a number N based on A called exponent X , to which you need to build A to get the number N
Provided that 
,
,
From the definition of logarithm it follows that 
, i.e.
- this equality is the basic logarithmic identity.
Logarithms to base 10 are called decimal logarithms. Instead of 
write 
.
Logarithms to the base e
are called natural and are designated 
.
Basic properties of logarithms.
The logarithm of one is equal to zero for any base.
The logarithm of the product is equal to the sum of the logarithms of the factors.
3) The logarithm of the quotient is equal to the difference of the logarithms
Factor 
called the modulus of transition from logarithms to the base a
to logarithms at the base b
.
Using properties 2-5, it is often possible to reduce the logarithm of a complex expression to the result of simple arithmetic operations on logarithms.
For example, 
Such transformations of a logarithm are called logarithms. Transformations inverse to logarithms are called potentiation.
Chapter 2. Elements of higher mathematics.
1. Limits
Limit of the function 
is a finite number A if, as xx
0
for each predetermined 
, there is such a number 
that as soon as 
, That 
.
A function that has a limit differs from it by an infinitesimal amount: 
, where- b.m.v., i.e. 
.
Example. Consider the function 
.
When striving 
, function y
tends to zero: 
1.1. Basic theorems about limits.
The limit of a constant value is equal to this constant value
.
The limit of the sum (difference) of a finite number of functions is equal to the sum (difference) of the limits of these functions.
The limit of the product of a finite number of functions is equal to the product of the limits of these functions.
The limit of the quotient of two functions is equal to the quotient of the limits of these functions if the limit of the denominator is not zero.
Wonderful Limits
,
, Where 
1.2. Limit Calculation Examples
However, not all limits are calculated so easily. More often, calculating the limit comes down to revealing an uncertainty of the type: 
or .
.
2. Derivative of a function
Let us have a function 
, continuous on the segment 
.
Argument 
got some increase 
. Then the function will receive an increment 
.
Argument value 
corresponds to the function value 
.
Argument value 
corresponds to the function value.
Hence, .
Let us find the limit of this ratio at 
. If this limit exists, then it is called the derivative of the given function.
Definition 3 Derivative of a given function 
by argument 
is called the limit of the ratio of the increment of a function to the increment of the argument, when the increment of the argument arbitrarily tends to zero.
Derivative of a function 
can be designated as follows:
;
;
;
.
Definition 4The operation of finding the derivative of a function is called differentiation.
2.1. Mechanical meaning of derivative.
Let's consider the rectilinear motion of some rigid body or material point.
Let at some point in time 
moving point 
was at a distance 
from the starting position 
.
After some period of time 
she moved a distance 
. Attitude 
=
- average speed of a material point 
. Let us find the limit of this ratio, taking into account that 
.
Consequently, determining the instantaneous speed of movement of a material point is reduced to finding the derivative of the path with respect to time.
2.2. Geometric value of the derivative
Let us have a graphically defined function 
.
Rice. 1. Geometric meaning of derivative
If 
, then point 
, will move along the curve, approaching the point 
.
Hence 
, i.e. the value of the derivative for a given value of the argument 
numerically equal to the tangent of the angle formed by the tangent at a given point with the positive direction of the axis 
.
2.3. Table of basic differentiation formulas.
Power function
|
|
|
|
|
|
|
Exponential function
|
|
|
|
|
Logarithmic function
|
|
|
|
|
Trigonometric function
|
|
|
|
|
|
|
|
|
|
Inverse trigonometric function
|
|
|
|
|
|
|
|
|
|
2.4. Rules of differentiation.
Derivative of 
Derivative of the sum (difference) of functions
Derivative of the product of two functions
Derivative of the quotient of two functions
2.5. Derivative of a complex function.
Let the function be given 
such that it can be represented in the form
And 
, where the variable 
is an intermediate argument, then 
The derivative of a complex function is equal to the product of the derivative of the given function with respect to the intermediate argument and the derivative of the intermediate argument with respect to x.
Example 1. 
Example 2. 
3. Differential function.
Let there be 
, differentiable on some interval 
let it go at
this function has a derivative
,
then we can write
(1),
Where 
- an infinitesimal quantity,
since when 
Multiplying all terms of equality (1) by 
we have:
Where 
- b.m.v. higher order.
Magnitude 
called the differential of the function 
and is designated 
.
3.1. Geometric value of the differential.
Let the function be given 
.
Fig.2. Geometric meaning of differential.
.
Obviously, the differential of the function 
is equal to the increment of the ordinate of the tangent at a given point.
3.2. Derivatives and differentials of various orders.
If there 
, Then 
is called the first derivative.
The derivative of the first derivative is called the second-order derivative and is written 
.
Derivative of the nth order of the function 
is called the (n-1)th order derivative and is written:
.
The differential of the differential of a function is called the second differential or second order differential.
.
.
3.3 Solving biological problems using differentiation.
Task 1. Studies have shown that the growth of a colony of microorganisms obeys the law 
, Where N
– number of microorganisms (in thousands), t
– time (days).
b) Will the population of the colony increase or decrease during this period?
Answer. The size of the colony will increase.
Task 2. The water in the lake is periodically tested to monitor the content of pathogenic bacteria. Through t days after testing, the concentration of bacteria is determined by the ratio
.
When will the lake have a minimum concentration of bacteria and will it be possible to swim in it?
Solution: A function reaches max or min when its derivative is zero.
,
Let's determine the max or min will be in 6 days. To do this, let's take the second derivative.
Answer: After 6 days there will be a minimum concentration of bacteria.
The logarithm of a number b to base a is the exponent to which the number a must be raised to obtain the number b.
If, then.
Logarithm - extreme important mathematical quantity, since logarithmic calculus allows not only solving exponential equations, but also operating with exponents, differentiating exponential and logarithmic functions, integrating them and leading them to a more acceptable form to be calculated.
In contact with
All properties of logarithms are directly related to the properties of exponential functions. For example, the fact that 
means that:
It should be noted that when solving specific problems, the properties of logarithms may turn out to be more important and useful than the rules for working with powers.
Let us present some identities:
Here are the basic algebraic expressions:
;
.
Attention! can exist only for x>0, x≠1, y>0.
Let's try to understand the question of what natural logarithms are. Special interest in mathematics represent two types- the first one has the number “10” as its base, and is called the “decimal logarithm”. The second one is called natural. The base of the natural logarithm is the number “e”. This is what we will talk about in detail in this article.
Designations:
- lg x - decimal;
- ln x - natural.
Using the identity, we can see that ln e = 1, as well as the fact that lg 10=1.
Natural logarithm graph
Let's construct a graph of the natural logarithm using the standard classical method point by point. If you wish, you can check whether we are constructing the function correctly by examining the function. However, it makes sense to learn how to build it “manually” in order to know how to correctly calculate the logarithm.
Function: y = ln x. Let's write down a table of points through which the graph will pass:
Let us explain why we chose these particular values of the argument x. It's all about identity: . For the natural logarithm this identity will look like this:
For convenience, we can take five reference points:
;
;
.
;
.
Thus, calculating natural logarithms is a fairly simple task; moreover, it simplifies calculations of operations with powers, turning them into ordinary multiplication.
By plotting a graph point by point, we get an approximate graph:
The domain of definition of the natural logarithm (i.e., all valid values of the argument X) is all numbers greater than zero.
Attention! The domain of definition of the natural logarithm includes only positive numbers! The scope of definition does not include x=0. This is impossible based on the conditions for the existence of the logarithm.
The range of values (i.e. all valid values of the function y = ln x) is all numbers in the interval.
Natural log limit
Studying the graph, the question arises - how does the function behave at y<0.
Obviously, the graph of the function tends to cross the y-axis, but will not be able to do this, since the natural logarithm of x<0 не существует.
Limit of natural log can be written this way:
Formula for replacing the base of a logarithm
Dealing with a natural logarithm is much easier than dealing with a logarithm that has an arbitrary base. That is why we will try to learn how to reduce any logarithm to a natural one, or express it to an arbitrary base through natural logarithms.
Let's start with the logarithmic identity:
Then any number or variable y can be represented as:
where x is any number (positive according to the properties of the logarithm).
This expression can be taken logarithmically on both sides. Let's do this using an arbitrary base z:
Let’s use the property (only instead of “c” we have the expression):
From here we get the universal formula:
.
In particular, if z=e, then:
.
We were able to represent a logarithm to an arbitrary base through the ratio of two natural logarithms.
We solve problems
In order to better understand natural logarithms, let's look at examples of several problems.
Problem 1. It is necessary to solve the equation ln x = 3.
Solution: Using the definition of the logarithm: if , then , we get:
Problem 2. Solve the equation (5 + 3 * ln (x - 3)) = 3.
Solution: Using the definition of the logarithm: if , then , we get:
.
Let's use the definition of a logarithm again:
.
Thus:
.
You can approximately calculate the answer, or you can leave it in this form.
Task 3. Solve the equation.
Solution: Let's make a substitution: t = ln x. Then the equation will take the following form:
.
We have a quadratic equation. Let's find its discriminant:
First root of the equation:
.
Second root of the equation:
.
Remembering that we made the substitution t = ln x, we get:
In statistics and probability theory, logarithmic quantities are found very often. This is not surprising, because the number e often reflects the growth rate of exponential quantities.
In computer science, programming and computer theory, logarithms are encountered quite often, for example, in order to store N bits in memory.
In the theories of fractals and dimensions, logarithms are constantly used, since the dimensions of fractals are determined only with their help.
In mechanics and physics There is no section where logarithms were not used. Barometric distribution, all the principles of statistical thermodynamics, the Tsiolkovsky equation, etc. are processes that can be mathematically described only using logarithms.
In chemistry, logarithms are used in Nernst equations and descriptions of redox processes.
Amazingly, even in music, in order to find out the number of parts of an octave, logarithms are used.
Natural logarithm Function y=ln x its properties
Proof of the main property of the natural logarithm
