Calculator for solving systems of inequalities. Systems of linear inequalities

System of inequalities.
Example 1. Find the domain of an expression
Solution. Under the square root sign there should be no a negative number, which means that two inequalities must be satisfied simultaneously: In such cases, they say that the problem reduces to solving a system of inequalities

But we have not yet encountered such a mathematical model (system of inequalities). This means that we are not yet able to complete the solution to the example.

The inequalities that form a system are combined with a curly bracket (the same is true in systems of equations). For example, record

means that the inequalities 2x - 1 > 3 and 3x - 2< 11 образуют систему неравенств.

Sometimes a system of inequalities is written in the form of a double inequality. For example, a system of inequalities

can be written as a double inequality 3<2х-1<11.

In the 9th grade algebra course, we will consider only systems of two inequalities.

Consider the system of inequalities

You can select several of its particular solutions, for example x = 3, x = 4, x = 3.5. In fact, for x = 3 the first inequality takes the form 5 > 3, and the second one takes the form 7< 11. Получились два верных числовых неравенства, значит, х = 3 - решение системы неравенств. Точно так же можно убедиться в том, что х = 4, х = 3,5 - решения системы неравенств.

At the same time, the value x = 5 is not a solution to the system of inequalities. When x = 5, the first inequality takes the form 9 > 3 - a correct numerical inequality, and the second one takes the form 13< 11- неверное числовое неравенство .
To solve a system of inequalities means to find all its particular solutions. It is clear that the guessing demonstrated above is not a method for solving a system of inequalities. IN following example We will show how people usually reason when solving a system of inequalities.

Example 3. Solve the system of inequalities:

Solution.

A) Solving the first inequality of the system, we find 2x > 4, x > 2; solving the second inequality of the system, we find 3x< 13 Отметим эти промежутки на одной координатной прямой , использовав для выделения первого промежутка верхнюю штриховку, а для второго - нижнюю штриховку (рис. 22). Решением системы неравенств будет пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали. В рассматриваемом примере получаем интервал
b) Solving the first inequality of the system, we find x > 2; solving the second inequality of the system, we find Let's mark these intervals on one coordinate line, using upper hatching for the first interval, and lower hatching for the second (Fig. 23). The solution to the system of inequalities will be the intersection of the solutions to the system’s inequalities, i.e. the interval where both hatches coincide. In the example under consideration we obtain a beam

V) Solving the first inequality of the system, we find x< 2; решая второе неравенство системы, находим Отметим эти промежутки на одной координатной прямой, использовав для первого промежутка верхнюю штриховку, а для второго - нижнюю штриховку (рис. 24). Решением системы неравенств будет пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали. Здесь такого промежутка нет, значит, система неравенств не имеет решений.

Let us generalize the reasoning carried out in the example considered. Suppose we need to solve the system of inequalities

Let, for example, the interval (a, b) be a solution to the inequality fx 2 > g(x), and the interval (c, d) be a solution to the inequality f 2 (x) > s 2 (x). Let's mark these intervals on one coordinate line, using upper hatching for the first interval, and lower hatching for the second (Fig. 25). The solution to a system of inequalities is the intersection of solutions to the system’s inequalities, i.e. the interval where both hatches coincide. In Fig. 25 is the interval (c, b).

Now we are without special labor we can solve the system of inequalities that we obtained above in example 1:

Solving the first inequality of the system, we find x > 2; solving the second inequality of the system, we find x< 8. Отметим эти промежутки (лучи) на одной координатной прямой, использовав для первого -верхнюю, а для второго - нижнюю штриховку (рис. 26). Решением системы неравенств будет пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали, - отрезок . Это - область определения того выражения, о котором шла речь в примере 1.

Of course, the system of inequalities does not necessarily have to consist of linear inequalities, as has been the case so far; Any rational (and not only rational) inequalities can occur. Technically, working with a system of rational nonlinear inequalities is, of course, more complicated, but there is nothing fundamentally new (compared to systems of linear inequalities) here.

Example 4. Solve the system of inequalities

Solution.

1) Solve the inequality We have
Let's mark points -3 and 3 on the number line (Fig. 27). They divide the line into three intervals, and on each interval the expression p(x) = (x- 3)(x + 3) retains a constant sign - these signs are indicated in Fig. 27. We are interested in the intervals at which the inequality p(x) > 0 holds (they are shaded in Fig. 27), and the points at which the equality p(x) = 0 holds, i.e. points x = -3, x = 3 (they are marked in Fig. 2 7 with dark circles). Thus, in Fig. Figure 27 presents a geometric model for solving the first inequality.

2) Solve the inequality We have
Let's mark points 0 and 5 on the number line (Fig. 28). They divide the line into three intervals, and on each interval the expression<7(х) = х(5 - х) сохраняет постоянный знак - эти знаки указаны на рис. 28. Нас интересуют промежутки, на которых выполняется неравенство g(х) >O (shaded in Fig. 28), and the points at which the equality g (x) - O is satisfied, i.e. points x = 0, x = 5 (they are marked in Fig. 28 with dark circles). Thus, in Fig. Figure 28 presents a geometric model for solving the second inequality of the system.

3) Let us mark the found solutions to the first and second inequalities of the system on the same coordinate line, using upper hatching for solutions to the first inequality, and lower hatching for solutions to the second (Fig. 29). The solution to the system of inequalities will be the intersection of the solutions to the system’s inequalities, i.e. the interval where both hatches coincide. Such an interval is a segment.

Example 5. Solve the system of inequalities:

Solution:

A) From the first inequality we find x >2. Let's consider the second inequality. The square trinomial x 2 + x + 2 does not have real roots, and its leading coefficient (coefficient at x 2) is positive. This means that for all x the inequality x 2 + x + 2>0 holds, and therefore the second inequality of the system has no solutions. What does this mean for the system of inequalities? This means that the system has no solutions.

b) From the first inequality we find x > 2, and the second inequality is satisfied for any values ​​of x. What does this mean for the system of inequalities? This means that its solution has the form x>2, i.e. coincides with the solution to the first inequality.

Answer:

a) no solutions; b) x >2.

This example is an illustration of the following useful

1. If in a system of several inequalities with one variable one inequality has no solutions, then the system has no solutions.

2. If in a system of two inequalities with one variable, one inequality is satisfied for any values ​​of the variable, then the solution to the system is the solution to the second inequality of the system.

Concluding this section, let us return to the problem about the intended number given at the beginning and solve it, as they say, according to all the rules.

Example 2(see p. 29). Intended natural number. It is known that if you add 13 to the square of the intended number, then the sum will be greater than the product of the intended number and the number 14. If you add 45 to the square of the intended number, then the sum will be less product the planned number and the number 18. What number is planned?

Solution.

First stage. Drawing up a mathematical model.
The intended number x, as we saw above, must satisfy the system of inequalities

Second phase. Working with the compiled mathematical model. Let's transform the first inequality of the system to the form
x2- 14x+ 13 > 0.

Let's find the roots of the trinomial x 2 - 14x + 13: x 2 = 1, x 2 = 13. Using the parabola y = x 2 - 14x + 13 (Fig. 30) we conclude that the inequality we are interested in is satisfied at x< 1 или x > 13.

Let us transform the second inequality of the system to the form x2 - 18 2 + 45< 0. Найдем корни трехчлена х 2 - 18x + 45: = 3, х 2 = 15.

This article provides initial information about systems of inequalities. Here is a definition of a system of inequalities and a definition of a solution to a system of inequalities. The main types of systems that most often have to be worked with in algebra lessons at school are also listed, and examples are given.

Page navigation.

What is a system of inequalities?

It is convenient to define systems of inequalities in the same way as we introduced the definition of a system of equations, that is, by the type of notation and the meaning embedded in it.

Definition.

System of inequalities is a record that represents a certain number of inequalities written one below the other, united on the left by a curly brace, and denotes the set of all solutions that are simultaneously solutions to each inequality of the system.

Let us give an example of a system of inequalities. Let's take two arbitrary ones, for example, 2 x−3>0 and 5−x≥4 x−11, write them one below the other
2 x−3>0 ,
5−x≥4 x−11
and unite with a system sign - a curly brace, as a result we obtain a system of inequalities of the following form:

A similar idea is given about systems of inequalities in school textbooks. It is worth noting that their definitions are given more narrowly: for inequalities with one variable or with two variables.

Main types of systems of inequalities

It is clear that it is possible to create infinitely many different systems of inequalities. In order not to get lost in this diversity, it is advisable to consider them in groups that have their own features. All systems of inequalities can be divided into groups according to the following criteria:

• by the number of inequalities in the system;
• by the number of variables involved in the recording;
• by the type of inequalities themselves.

Based on the number of inequalities included in the record, systems of two, three, four, etc. are distinguished. inequalities In the previous paragraph we gave an example of a system, which is a system of two inequalities. Let us show another example of a system of four inequalities .

Separately, we will say that there is no point in talking about a system of one inequality, in this case, essentially we're talking about about inequality itself, not about the system.

If you look at the number of variables, then there are systems of inequalities with one, two, three, etc. variables (or, as they also say, unknowns). Look at the last system of inequalities written two paragraphs above. It is a system with three variables x, y and z. Please note that her first two inequalities do not contain all three variables, but only one of them. In the context of this system, they should be understood as inequalities with three variables of the form x+0·y+0·z≥−2 and 0·x+y+0·z≤5, respectively. Note that the school focuses on inequalities with one variable.

It remains to discuss what types of inequalities are involved in recording systems. At school, they mainly consider systems of two inequalities (less often - three, even less often - four or more) with one or two variables, and the inequalities themselves are usually entire inequalities first or second degree (less often - more high degrees or fractionally rational). But don’t be surprised if in your preparation materials for the Unified State Exam you come across systems of inequalities containing irrational, logarithmic, exponential and other inequalities. As an example, we give the system of inequalities , it is taken from .

What is the solution to a system of inequalities?

Let us introduce another definition related to systems of inequalities - the definition of a solution to a system of inequalities:

Definition.

Solving a system of inequalities with one variable is called such a value of a variable that turns each of the inequalities of the system into true, in other words, it is a solution to each inequality of the system.

Let's explain with an example. Let's take a system of two inequalities with one variable. Let's take the value of the variable x equal to 8, it is a solution to our system of inequalities by definition, since its substitution into the inequalities of the system gives two correct numerical inequalities 8>7 and 2−3·8≤0. On the contrary, unity is not a solution to the system, since when it is substituted for the variable x, the first inequality will turn into the incorrect numerical inequality 1>7.

Similarly, one can introduce the definition of a solution to a system of inequalities with two, three and a large number variables:

Definition.

Solving a system of inequalities with two, three, etc. variables called a pair, three, etc. values ​​of these variables, which at the same time is a solution to every inequality of the system, that is, turns every inequality of the system into a correct numerical inequality.

For example, a pair of values ​​x=1, y=2 or in another notation (1, 2) is a solution to a system of inequalities with two variables, since 1+2<7 и 1−2<0 - верные числовые неравенства. А пара (3,5, 3) не является решением этой системы, так как второе неравенство при этих значениях переменных дает неверное числовое неравенство 3,5−3<0 .

Systems of inequalities may have no solutions, may have a finite number of solutions, or may have an infinite number of solutions. People often talk about the set of solutions to a system of inequalities. When a system has no solutions, then there is an empty set of its solutions. When there are a finite number of solutions, then the set of solutions contains a finite number of elements, and when there are infinitely many solutions, then the set of solutions consists of an infinite number of elements.

Some sources introduce definitions of a particular and general solution to a system of inequalities, as, for example, in Mordkovich's textbooks. Under private solution of the system of inequalities understand her one single decision. In its turn general solution to the system of inequalities- these are all her private decisions. However, these terms make sense only when it is necessary to specifically emphasize what kind of solution we are talking about, but usually this is already clear from the context, so much more often they simply say “a solution to a system of inequalities.”

From the definitions of a system of inequalities and its solutions introduced in this article, it follows that a solution to a system of inequalities is the intersection of the sets of solutions to all inequalities of this system.

Bibliography.

1. Algebra: textbook for 8th grade. general education institutions / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; edited by S. A. Telyakovsky. - 16th ed. - M.: Education, 2008. - 271 p. : ill. - ISBN 978-5-09-019243-9.
2. Algebra: 9th grade: educational. for general education institutions / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; edited by S. A. Telyakovsky. - 16th ed. - M.: Education, 2009. - 271 p. : ill. - ISBN 978-5-09-021134-5.
3. Mordkovich A. G. Algebra. 9th grade. In 2 hours. Part 1. Textbook for students of general education institutions / A. G. Mordkovich, P. V. Semenov. - 13th ed., erased. - M.: Mnemosyne, 2011. - 222 p.: ill. ISBN 978-5-346-01752-3.
4. Mordkovich A. G. Algebra and beginning of mathematical analysis. Grade 11. In 2 hours. Part 1. Textbook for students of general education institutions (profile level) / A. G. Mordkovich, P. V. Semenov. - 2nd ed., erased. - M.: Mnemosyne, 2008. - 287 p.: ill. ISBN 978-5-346-01027-2.
5. Unified State Exam-2013. Mathematics: standard exam options: 30 options / ed. A. L. Semenova, I. V. Yashchenko. – M.: Publishing House “National Education”, 2012. – 192 p. – (USE-2013. FIPI - school).

An inequality is two numbers or mathematical expressions connected by one of the signs: > (greater than, in the case of strict inequalities),< (меньше, в случае строгих неравенств), ≥ (больше или равно, в случае нестрогих неравенств), ≤ (меньше или равно, в случае нестрогих неравенств).

Inequality is linear under the same conditions as the equation: it contains variables only to the first degree and does not contain products of variables.

The solution to linear inequalities and systems of linear inequalities is inextricably linked with their geometric meaning: the solution to a linear inequality is a certain half-plane into which the entire plane is divided by a straight line, the equation of which defines the linear inequality. This half-plane, and in the case of a system of linear inequalities, the part of the plane limited by several straight lines, must be found in the drawing.

Many economic problems, in particular, linear programming problems, in which it is required to find the maximum or minimum of a function, are reduced to solving systems of linear inequalities with a large number of variables.

Solving systems of linear inequalities with any number of unknowns

First, let's look at linear inequalities in the plane. Consider one inequality with two variables and :

,

where are the coefficients of the variables (some numbers), is the free term (also some number).

One inequality with two unknowns, like an equation, has an infinite number of solutions. The solution to this inequality is a pair of numbers that satisfy this inequality. Geometrically, the set of solutions to an inequality is depicted as a half-plane bounded by a straight line

,

which we will call the boundary line.

Step 1. Construct a line that bounds the set of solutions to a linear inequality

To do this, you need to know any two points on this line. Let's find the points of intersection with the coordinate axes. Intersection ordinate A equal to zero (Figure 1). The numerical values ​​on the axes in this figure refer to example 1, which we will analyze immediately after this theoretical excursion.

We find the abscissa by solving the equation of the line with the equation of the axis as a system.

Let's find the intersection with the axis:

Substituting the value into the first equation, we get

Where .

Thus, we found the abscissa of the point A .

Let's find the coordinates of the point of intersection with the axis.

Abscissa dots B equal to zero. Let us solve the equation of the boundary line with the equation of the coordinate axis:

,

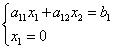
therefore, the coordinates of the point B: .

Step 2. Draw a straight line limiting the set of solutions to the inequality. Knowing the points A And B intersection of the boundary line with the coordinate axes, we can draw this line. A straight line (again Figure 1) divides the entire plane into two parts lying to the right and left (above and below) of this straight line.

Step 3. Determine which half-plane is the solution to this inequality. To do this, you need to substitute the origin of coordinates (0; 0) into this inequality. If the coordinates of the origin satisfy the inequality, then the solution to the inequality is the half-plane in which the origin of coordinates is located. If the coordinates do not satisfy the inequality, then the solution to the inequality is a half-plane that does not contain the origin. The half-plane of the solution to the inequality will be denoted by strokes from the straight line into the half-plane, as in Figure 1.

If we solve a system of linear inequalities, then each step is performed for each of the system inequalities.

Example 1. Solve inequality

Solution. Let's draw a straight line

Substituting a straight line into the equation, we get , and substituting , we get . Therefore, the coordinates of the points of intersection with the axes will be A(3; 0) , B(0; 2) . Let's draw a straight line through these points (again, Figure 1).

Let us choose a half-plane of solutions to the inequality. To do this, we substitute the coordinates of the origin (0; 0) into the inequality:

we obtain , i.e. the coordinates of the origin satisfy this inequality. Consequently, the solution to the inequality is the half-plane containing the origin of coordinates, i.e., the left (aka lower) half-plane.

If this inequality were strict, that is, it would have the form

then the points of the boundary line would not be a solution, since they do not satisfy the inequality.

Now consider a system of linear inequalities with two unknowns:

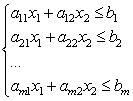
Each of the inequalities of this system on the plane defines a half-plane. A system of linear inequalities is called consistent if it has at least one solution, and inconsistent if it has no solutions. A solution to a system of linear inequalities is any pair of numbers () that satisfies all the inequalities of the given system.

Geometrically, the solution to a system of linear inequalities is the set of points that satisfy all the inequalities of the system, that is, the common part of the resulting half-planes. Therefore, geometrically, in the general case, the solution can be depicted in the form of some polygon; in a particular case, it can be a line, a segment, or even a point. If a system of linear inequalities is inconsistent, then there is not a single point on the plane that satisfies all the inequalities of the system.

Example 2.

Solution. So, we need to find a polygon of solutions to this system of inequalities. Let's construct a boundary line for the first inequality, that is, a line, and a boundary line for the second inequality, that is, a line.

We do this step by step, as was shown in the theoretical reference and in example 1, especially since in example 1 we built a boundary line for the inequality, which is the first in this system.

The half-planes of solutions corresponding to the inequalities of this system are shaded inward in Figure 2. The common part of the solution half-planes is an open angle ABC. This means that the set of points in the plane that make up an open angle ABC, is a solution to both the first and second inequalities of the system, that is, it is a solution to a system of two linear inequalities. In other words, the coordinates of any point from this set satisfy both inequalities of the system.

Example 3. Solve a system of linear inequalities

Solution. Let us construct boundary lines corresponding to the inequalities of the system. We do this by following the steps given in the theoretical help for each inequality. Now we determine the half-planes of solutions for each inequality (Figure 3).

The half-planes of solutions corresponding to the inequalities of a given system are shaded inward. The intersection of half-planes of solutions is depicted, as shown in the figure, in the form of a quadrilateral ABCE. We found that the polygon of solutions to a system of linear inequalities with two variables is a quadrilateral ABCE .

Everything described above about systems of linear inequalities with two unknowns also applies to systems of inequalities with any number of unknowns, with the only difference that the solution to the inequality with n the unknowns will be the totality n numbers () satisfying all inequalities, and instead of the boundary line there will be a boundary hyperplane n-dimensional space. The solution will be a solution polyhedron (simplex) bounded by hyperplanes.

In the article we will consider solving inequalities. We will tell you clearly about how to construct a solution to inequalities, with clear examples!

Before we look at solving inequalities using examples, let’s understand the basic concepts.

General information about inequalities

Inequality is an expression in which functions are connected by relation signs >, . Inequalities can be both numerical and literal.
Inequalities with two signs of the ratio are called double, with three - triple, etc. For example:
a(x) > b(x),
a(x) a(x) b(x),
a(x) b(x).
a(x) Inequalities containing the sign > or or - are not strict.
Solving the inequality is any value of the variable for which this inequality will be true.
"Solve inequality" means that we need to find the set of all its solutions. There are different methods for solving inequalities. For inequality solutions They use the number line, which is infinite. For example, solution to inequality x > 3 is the interval from 3 to +, and the number 3 is not included in this interval, therefore the point on the line is denoted by an empty circle, because inequality is strict.
+
The answer will be: x (3; +).
The value x=3 is not included in the solution set, so the parenthesis is round. The infinity sign is always highlighted with a parenthesis. The sign means "belonging."
Let's look at how to solve inequalities using another example with a sign:
x 2
-+
The value x=2 is included in the set of solutions, so the bracket is square and the point on the line is indicated by a filled circle.
The answer will be: x " title="Rendered by QuickLaTeX.com">!}

To solve a system, you need each of its constituent inequalities. Only the decision was made not to write separately, but together, combining them with a curly brace.

In each of the inequalities of the system, we move the unknowns to one side, the known ones to the other with opposite sign:

Title="Rendered by QuickLaTeX.com">!}

After simplification, both sides of the inequality must be divided by the number in front of X. We divide the first inequality by positive number, so the inequality sign does not change. We divide the second inequality by a negative number, so the inequality sign must be reversed:

Title="Rendered by QuickLaTeX.com">!}

We mark the solution to the inequalities on the number lines:

In response, we write down the intersection of the solutions, that is, the part where there is shading on both lines.

Answer: x∈[-2;1).

In the first inequality, let's get rid of the fraction. To do this, we multiply both sides term by term by the least common denominator 2. When multiplied by a positive number, the inequality sign does not change.

In the second inequality we open the brackets. The product of the sum and the difference of two expressions is equal to the difference of the squares of these expressions. On the right side is the square of the difference between the two expressions.

Title="Rendered by QuickLaTeX.com">!}

We move the unknowns to one side, the known ones to the other with the opposite sign and simplify:

We divide both sides of the inequality by the number in front of X. In the first inequality, we divide by a negative number, so the sign of the inequality is reversed. In the second, we divide by a positive number, the inequality sign does not change:

Title="Rendered by QuickLaTeX.com">!}

Both inequalities have a “less than” sign (it doesn’t matter that one sign is strictly “less than”, the other is loose, “less than or equal”). We can not mark both solutions, but use the “ “ rule. The smaller one is 1, therefore the system reduces to the inequality

We mark its solution on the number line:

Answer: x∈(-∞;1].

Opening the parentheses. In the first inequality - . It is equal to the sum of the cubes of these expressions.

In the second, the product of the sum and the difference of two expressions, which is equal to the difference of squares. Since here there is a minus sign in front of the brackets, it is better to open them in two stages: first use the formula, and only then open the brackets, changing the sign of each term to the opposite.

We move the unknowns in one direction, the knowns in the other with the opposite sign:

Title="Rendered by QuickLaTeX.com">!}

Both are greater than signs. Using the “more than more” rule, we reduce the system of inequalities to one inequality. The larger of the two numbers is 5, therefore,

Title="Rendered by QuickLaTeX.com">!}

We mark the solution to the inequality on the number line and write down the answer:

Answer: x∈(5;∞).

Since in algebra systems of linear inequalities occur not only as independent tasks, but also in the course of solving various kinds equations, inequalities, etc., it is important to master this topic in time.

Next time we will look at examples of solving systems of linear inequalities in special cases when one of the inequalities has no solutions or its solution is any number.