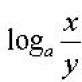Limits online. Determining the final limit of a sequence
Theory of limits- one of the sections of mathematical analysis that some can master, while others have difficulty calculating the limits. The question of finding limits is quite general, since there are dozens of techniques solution limits various types. The same limits can be found both using L'Hopital's rule and without it. It happens that scheduling a series of infinitesimal functions allows you to quickly obtain desired result. There are a set of techniques and tricks that allow you to find the limit of a function of any complexity. In this article we will try to understand the main types of limits that are most often encountered in practice. We will not give the theory and definition of the limit here; there are many resources on the Internet where this is discussed. Therefore, let’s get down to practical calculations, this is where your “I don’t know! I can’t! We weren’t taught!”
Calculating limits using the substitution method
Example 1. Find the limit of a function
Lim((x^2-3*x)/(2*x+5),x=3).
Solution: Examples of this kind can be theoretically calculated using the usual substitution
The limit is 18/11.
There is nothing complicated or wise about such limits - we substituted the value, calculated it, and wrote down the limit as an answer. However, based on such limits, everyone is taught that first of all they need to substitute the value into the function. Further, the limits become more complicated, introducing the concept of infinity, uncertainty, and the like.
A limit with uncertainty like infinity divided by infinity. Uncertainty Disclosure Techniques
Example 2. Find the limit of a function
Lim((x^2+2x)/(4x^2+3x-4),x=infinity).
Solution: A limit of the form polynomial divided by a polynomial is given, and the variable tends to infinity ![]()
Simply substituting the value to which the variable should be found to find the limits will not help, we get an uncertainty of the form infinity divided by infinity.
According to the theory of limits, the algorithm for calculating the limit is to find the largest power of “x” in the numerator or denominator. Next, the numerator and denominator are simplified to it and the limit of the function is found 
Since the value tends to zero when the variable approaches infinity, they are neglected, or written into the final expression in the form of zeros 
Immediately from practice, you can get two conclusions that are a hint in the calculations. If a variable tends to infinity and the degree of the numerator is greater than the degree of the denominator, then the limit is equal to infinity. Otherwise, if the polynomial in the denominator is of higher order than in the numerator, the limit is zero.
The limit can be written in formulas like this: 
If we have a function of the form an ordinary field without fractions, then its limit is equal to infinity ![]()
The next type of limits concerns the behavior of functions near zero.
Example 3. Find the limit of a function
Lim((x^2+3x-5)/(x^2+x+2), x=0).
Solution: There is no need to remove the leading factor of the polynomial here. Exactly the opposite, you need to find the smallest power of the numerator and denominator and calculate the limit ![]()
Value x^2; x tend to zero when the variable tends to zero. Therefore, they are neglected, so we get ![]()
that the limit is 2.5.
Now you know how to find the limit of a function of the form, divide a polynomial by a polynomial if the variable tends to infinity or 0. But this is only a small and easy part of the examples. From the following material you will learn how to uncover uncertainties in the limits of a function.
Limit with uncertainty of type 0/0 and methods for its calculation
Everyone immediately remembers the rule that you cannot divide by zero. However, the theory of limits in this context implies infinitesimal functions.
Let's look at a few examples for clarity.
Example 4. Find the limit of a function
Lim((3x^2+10x+7)/(x+1), x=-1).
Solution: When we substitute the value of the variable x = -1 into the denominator, we get zero, and we get the same thing in the numerator. So we have uncertainty of the form 0/0.
Dealing with such uncertainty is simple: you need to factorize the polynomial, or rather, select the factor that turns the function into zero. 
After expansion, the limit of the function can be written as 
That's the whole method for calculating the limit of a function. We do the same if there is a limit of the form polynomial divided by a polynomial.
Example 5. Find the limit of a function
Lim((2x^2-7x+6)/(3x^2-x-10), x=2).
Solution: Direct substitution shows
2*4-7*2+6=0;
3*4-2-10=0
what do we have type 0/0 uncertainty.
Let's divide the polynomials by the factor that introduces the singularity ![]()
![]()
There are teachers who teach that polynomials of 2nd order, that is, the “quadratic equations” type, should be solved through the discriminant. But real practice shows that this is longer and more confusing, so get rid of the features within the limits according to the specified algorithm. Thus we write the function in the form prime factors and calculate to the limit 
As you can see, there is nothing complicated in calculating such limits. By the time you study the limits, you know how to divide polynomials, at least according to the program you should have already passed it.
Among the tasks on type 0/0 uncertainty There are some in which you need to use abbreviated multiplication formulas. But if you don’t know them, then by dividing a polynomial by a monomial you can get the desired formula.
Example 6. Find the limit of a function
Lim((x^2-9)/(x-3), x=3).
Solution: We have an uncertainty of type 0/0. In the numerator we use the abbreviated multiplication formula ![]()
and calculate the required limit ![]()
Method for revealing uncertainty by multiplying by its conjugate
The method is applied to the limits in which uncertainty is generated by irrational functions. The numerator or denominator turns to zero at the calculation point and it is not known how to find the boundary.
Example 7. Find the limit of a function
Lim((sqrt(x+2)-sqrt(7x-10))/(3x-6), x=2).
Solution: Let's represent the variable in the limit formula
When substituting, we obtain an uncertainty of type 0/0.
According to the theory of limits, the way to bypass this feature is to multiply the irrational expression by its conjugate. To ensure that the expression does not change, the denominator must be divided by the same value 
Using the difference of squares rule, we simplify the numerator and calculate the limit of the function
We simplify the terms that create the singularity in the limit and perform the substitution
Example 8. Find the limit of a function
Lim((sqrt(x-2)-sqrt(2x-5))/(3-x), x=3).
Solution: Direct substitution shows that the limit has a singularity of the form 0/0. ![]()
To expand, we multiply and divide by the conjugate of the numerator 
We write down the difference of squares
We simplify the terms that introduce the singularity and find the limit of the function
![]()
Example 9. Find the limit of a function
Lim((x^2+x-6)/(sqrt(3x-2)-2), x=2).
Solution: Substitute two into the formula ![]()
We get uncertainty 0/0.
The denominator must be multiplied by the conjugate expression, and the numerator must be solved quadratic equation or factorize, taking into account the singularity. Since it is known that 2 is a root, we find the second root using Vieta’s theorem
Thus, we write the numerator in the form ![]()
and substitute it into the limit
By reducing the difference of squares, we get rid of the singularities in the numerator and denominator
In this way, you can get rid of singularities in many examples, and the application should be noted wherever a given difference of roots turns into zero during substitution. Other types of limits concern exponential functions, infinitesimal functions, logarithms, special limits and other techniques. But you can read about this in the articles listed below about limits.
This online math calculator will help you if you need it calculate the limit of a function. Program solution limits not only gives the answer to the problem, it leads detailed solution with explanations, i.e. displays the limit calculation process.
This program may be useful for high school students secondary schools in preparation for tests and exams, when testing knowledge before the Unified State Exam, for parents to control the solution of many problems in mathematics and algebra. Or maybe it’s too expensive for you to hire a tutor or buy new textbooks? Or do you just want to get it done as quickly as possible? homework in mathematics or algebra? In this case, you can also use our programs with detailed solutions.
This way you can conduct your own training and/or training of yours. younger brothers or sisters, while the level of education in the field of problems being solved increases.
Enter a function expressionCalculate limit
It was discovered that some scripts necessary to solve this problem were not loaded, and the program may not work.
You may have AdBlock enabled.
In this case, disable it and refresh the page.
For the solution to appear, you need to enable JavaScript.
Here are instructions on how to enable JavaScript in your browser.
Because There are a lot of people willing to solve the problem, your request has been queued.
In a few seconds the solution will appear below.
Please wait sec...
If you noticed an error in the solution, then you can write about this in the Feedback Form.
Do not forget indicate which task you decide what enter in the fields.
Our games, puzzles, emulators:
A little theory.
Limit of the function at x->x 0
Let the function f(x) be defined on some set X and let the point \(x_0 \in X\) or \(x_0 \notin X\)
Let us take from X a sequence of points different from x 0:
x 1 , x 2 , x 3 , ..., x n , ... (1)
converging to x*. The function values at the points of this sequence also form a numerical sequence
f(x 1), f(x 2), f(x 3), ..., f(x n), ... (2)
and one can raise the question of the existence of its limit.
Definition. The number A is called the limit of the function f(x) at the point x = x 0 (or at x -> x 0), if for any sequence (1) of values of the argument x different from x 0 converging to x 0, the corresponding sequence (2) of values function converges to number A.
$$ \lim_(x\to x_0)( f(x)) = A $$
The function f(x) can have only one limit at the point x 0. This follows from the fact that the sequence
(f(x n)) has only one limit.
There is another definition of the limit of a function.
Definition The number A is called the limit of the function f(x) at the point x = x 0 if for any number \(\varepsilon > 0\) there is a number \(\delta > 0\) such that for all \(x \in X, \; x \neq x_0 \), satisfying the inequality \(|x-x_0| Using logical symbols, this definition can be written as
\((\forall \varepsilon > 0) (\exists \delta > 0) (\forall x \in X, \; x \neq x_0, \; |x-x_0| Note that the inequalities \(x \neq x_0 , \; |x-x_0| The first definition is based on the concept of the limit of a number sequence, so it is often called the definition “in the language of sequences.” The second definition is called the definition “in the language \(\varepsilon - \delta \)”.
These two definitions of the limit of a function are equivalent and you can use either of them depending on which is more convenient for solving a particular problem.
Note that the definition of the limit of a function “in the language of sequences” is also called the definition of the limit of a function according to Heine, and the definition of the limit of a function “in the language \(\varepsilon - \delta \)” is also called the definition of the limit of a function according to Cauchy.
Limit of the function at x->x 0 - and at x->x 0 +
In what follows, we will use the concepts of one-sided limits of a function, which are defined as follows.
Definition The number A is called the right (left) limit of the function f(x) at the point x 0 if for any sequence (1) converging to x 0, whose elements x n are greater (less than) x 0, the corresponding sequence (2) converges to A.
Symbolically it is written like this:
$$ \lim_(x \to x_0+) f(x) = A \; \left(\lim_(x \to x_0-) f(x) = A \right) $$
We can give an equivalent definition of one-sided limits of a function “in the language \(\varepsilon - \delta \)”:
Definition a number A is called the right (left) limit of the function f(x) at the point x 0 if for any \(\varepsilon > 0\) there is a \(\delta > 0\) such that for all x satisfying the inequalities \(x_0 Symbolic entries:
Solution online function limits. Find the limiting value of a function or functional sequence at a point, calculate ultimate the value of the function at infinity. determine the convergence of a number series and much more can be done thanks to our online service- . We allow you to find function limits online quickly and accurately. You yourself enter the function variable and the limit to which it tends, and our service carries out all the calculations for you, giving an accurate and simple answer. And for finding the limit online you can enter both number series and analytical functions containing constants in literal expression. In this case, the found limit of the function will contain these constants as constant arguments in the expression. Our service solves any complex problems of finding limits online, it is enough to indicate the function and the point at which it is necessary to calculate limit value of function. Calculating online limits, you can use various methods and rules for solving them, while checking the result obtained with solving limits online on the www.site, which will lead to the successful completion of the task - you will avoid your own mistakes and clerical errors. Or you can completely trust us and use our result in your work, without spending extra effort and time on independently calculating the limit of the function. We allow the entry of such limit values like infinity. It is necessary to enter a common member of a number sequence and www.site will calculate the value limit online to plus or minus infinity.
One of the basic concepts of mathematical analysis is function limit And sequence limit at a point and at infinity, it is important to be able to solve correctly limits. With our service this will not be difficult. A decision is made limits online within a few seconds, the answer is accurate and complete. The study of mathematical analysis begins with transition to the limit, limits used in almost all sections higher mathematics, so it's useful to have a server at hand for online limit solutions, which is the site.
Number sequence.
How ?
In this lesson we will learn a lot of interesting things from the life of members of a large community called Vkontakte number sequences. The topic under consideration relates not only to the course of mathematical analysis, but also touches on the basics discrete mathematics. In addition, the material will be required for mastering other sections of the tower, in particular, during the study number series And functional series. You can say trivially that this is important, you can say encouragingly that it’s simple, you can say many more routine phrases, but today the first one is unusually lazy school week, so it’s terribly breaking me to write the first paragraph =) I had already saved the file in my heart and was getting ready to sleep, when suddenly... my head was illuminated by the idea of a sincere confession, which incredibly lightened my soul and pushed me to continue tapping my fingers on the keyboard.
Let's take a break from summer memories and look into this fascinating and positive world of the new social network:
Concept of number sequence
First, let's think about the word itself: what is sequence? Sequence is when something follows something. For example, a sequence of actions, a sequence of seasons. Or when someone is located behind someone. For example, a sequence of people in a queue, a sequence of elephants on the path to a watering hole.
Let's clarify immediately characteristic features sequences. Firstly, sequence members are located strictly in a certain order. So, if two people in the queue are swapped, then this will already be other subsequence. Secondly, everyone sequence member You can assign a serial number: ![]()
It's the same with numbers. Let to each natural value according to some rule compliant real number. Then they say that a numerical sequence is given.
Yes, in mathematical problems, unlike life situations the sequence almost always contains infinitely many numbers.
Wherein:
called first member sequences;
– second member sequences;
– third member sequences;
…
– nth or common member sequences;
…
In practice, the sequence is usually given common term formula, For example:
– sequence of positive even numbers: 
Thus, the record uniquely determines all members of the sequence - this is the rule (formula) according to which natural values ![]() numbers are put into correspondence. Therefore, the sequence is often briefly denoted by a common term, and instead of “x” other Latin letters can be used, for example:
numbers are put into correspondence. Therefore, the sequence is often briefly denoted by a common term, and instead of “x” other Latin letters can be used, for example:
Sequence of positive odd numbers: 
Another common sequence: ![]()
As many have probably noticed, the “en” variable plays the role of a kind of counter.
In fact, we dealt with number sequences back in middle school. Let's remember arithmetic progression. I won’t rewrite the definition, let’s touch on the essence at specific example. Let be the first term, and – step arithmetic progression. Then:
– the second term of this progression;
– the third term of this progression;
- fourth; ![]() - fifth;
- fifth;
…
And, obviously, the nth term is given recurrent formula
Note : in a recurrent formula, each subsequent term is expressed in terms of the previous term or even in terms of a whole set of previous terms.
The resulting formula is of little use in practice - to get, say, to , you need to go through all the previous terms. And in mathematics, a more convenient expression for the nth term of an arithmetic progression has been derived: ![]() . In our case:
. In our case:
Substitute natural numbers into the formula and check the correctness of the numerical sequence constructed above.
Similar calculations can be made for geometric progression, the nth term of which is given by the formula , where is the first term, and – denominator progression. In math tasks, the first term is often equal to one.
progression sets the sequence ![]() ;
;
progression ![]() sets the sequence;
sets the sequence;
progression ![]() sets the sequence
sets the sequence ![]() ;
;
progression ![]() sets the sequence
sets the sequence ![]() .
.
I hope everyone knows that –1 to an odd power is equal to –1, and to an even power – one.
Progression is called infinitely decreasing, if (last two cases).
Let's add two new friends to our list, one of whom has just knocked on the monitor's matrix:
The sequence in mathematical jargon is called a “blinker”:
Thus, sequence members can be repeated. So, in the example considered, the sequence consists of two infinitely alternating numbers.
Does it happen that the sequence consists of identical numbers? Certainly. For example, it sets an infinite number of “threes”. For aesthetes, there is a case when “en” still formally appears in the formula:
Let's invite a simple friend to dance: ![]()
What happens when "en" increases to infinity? Obviously, the members of the sequence will be infinitely close approach zero. This is the limit of this sequence, which is written as follows:
If the limit of a sequence is zero, then it is called infinitesimal.
In the theory of mathematical analysis it is given strict definition of the sequence limit through the so-called epsilon neighborhood. The next article will be devoted to this definition, but for now let’s look at its meaning:
Let us depict on the number line the terms of the sequence and the neighborhood symmetric with respect to zero (limit): 
Now pinch the blue area with the edges of your palms and begin to reduce it, pulling it towards the limit (red point). A number is the limit of a sequence if FOR ANY pre-selected -neighborhood (as small as you like) will be inside it infinitely many members of the sequence, and OUTSIDE it - only final number of members (or none at all). That is, the epsilon neighborhood can be microscopic, and even smaller, but the “infinite tail” of the sequence sooner or later must fully enter the area.
The sequence is also infinitesimal: with the difference that its members do not jump back and forth, but approach the limit exclusively from the right.
Naturally, the limit can be equal to any other finite number, an elementary example: 
Here the fraction tends to zero, and accordingly, the limit is equal to “two”.
If the sequence there is a finite limit, then it is called convergent(in particular, infinitesimal at ). Otherwise - divergent, in this case, two options are possible: either the limit does not exist at all, or it is infinite. In the latter case, the sequence is called infinitely large. Let's gallop through the examples of the first paragraph:
Sequences ![]() are infinitely large, as their members confidently move towards “plus infinity”:
are infinitely large, as their members confidently move towards “plus infinity”: 
An arithmetic progression with the first term and step is also infinitely large: ![]()
By the way, any arithmetic progression also diverges, with the exception of the case with a zero step - when . The limit of such a sequence exists and coincides with the first term.
The sequences have a similar fate: 
Any infinitely decreasing geometric progression, as is clear from the name, infinitely small:
If the denominator of the geometric progression is , then the sequence is infinitely large:
If, for example, then the limit does not exist at all, since the members tirelessly jump either to “plus infinity” or to “minus infinity”. A common sense and Matan’s theorems suggest that if something strives somewhere, then this is the only cherished place.
After a little revelation ![]() it becomes clear that the “flashing light” is to blame for the uncontrollable throwing, which, by the way, diverges on its own.
it becomes clear that the “flashing light” is to blame for the uncontrollable throwing, which, by the way, diverges on its own.
Indeed, for a sequence it is easy to choose a -neighborhood that, say, only clamps the number –1. As a result, an infinite number of sequence members (“plus ones”) will remain outside this neighborhood. But by definition, the “infinite tail” of the sequence from a certain moment (natural number) must fully go into ANY vicinity of your limit. Conclusion: the sky is the limit.
Factorial is infinitely large sequence:
Moreover, it is growing by leaps and bounds, so it is a number that has more than 100 digits (digits)! Why exactly 70? On it my engineering microcalculator begs for mercy.
With a control shot, everything is a little more complicated, and we have just come to the practical part of the lecture, in which we will analyze combat examples:
But now you need to be able to solve the limits of functions, at least at the level of two basic lessons: Limits. Examples of solutions And Wonderful Limits. Because many solution methods will be similar. But, first of all, let’s analyze the fundamental differences between the limit of a sequence and the limit of a function: ![]()
In the limit of the sequence, the “dynamic” variable “en” can tend to only to “plus infinity”– towards increasing natural numbers ![]() .
.
In the limit of the function, “x” can be directed anywhere – to “plus/minus infinity” or to an arbitrary real number.
Subsequence discrete(discontinuous), that is, it consists of individual isolated members. One, two, three, four, five, the bunny went out for a walk. The argument of a function is characterized by continuity, that is, “X” smoothly, without incident, tends to one or another value. And, accordingly, the function values will also continuously approach their limit.
Because of discreteness within the sequences there are their own signature things, such as factorials, “flashing lights”, progressions, etc. And now I will try to analyze the limits that are specific to sequences.
Let's start with progressions:
Example 1
Find the limit of the sequence ![]()
Solution: something similar to an infinitely decreasing geometric progression, but is it really that? For clarity, let’s write down the first few terms: 
Since, then we are talking about amount terms of an infinitely decreasing geometric progression, which is calculated by the formula.
Let's make a decision:
![]()
We use the formula for the sum of an infinitely decreasing geometric progression: . IN in this case: – the first term, – the denominator of the progression.

Example 2
Write the first four terms of the sequence and find its limit ![]()
This is an example for you to solve on your own. To eliminate the uncertainty in the numerator, you will need to apply the formula for the sum of the first terms of an arithmetic progression: ![]() , where is the first and a is the nth term of the progression.
, where is the first and a is the nth term of the progression.
Since within sequences "en" always tends to "plus infinity", it is not surprising that uncertainty is one of the most popular.
And many examples are solved in exactly the same way as function limits!
Or maybe something more complicated like  ? Check out Example No. 3 of the article Methods for solving limits.
? Check out Example No. 3 of the article Methods for solving limits.
From a formal point of view, the difference will be only in one letter - “x” here, and “en” here.
The technique is the same - the numerator and denominator must be divided by “en” to the highest degree.
Also, uncertainty within sequences is quite common. How to solve limits like ![]() can be found in Examples No. 11-13 of the same article.
can be found in Examples No. 11-13 of the same article.
To understand the limit, refer to Example No. 7 of the lesson Wonderful Limits(second wonderful limit is also valid for the discrete case). The solution will again be like a carbon copy with a single letter difference.
The next four examples (Nos. 3-6) are also “two-faced”, but in practice for some reason they are more characteristic of sequence limits than of function limits:
Example 3
Find the limit of the sequence ![]()
Solution: first the complete solution, then step-by-step comments: 
(1) In the numerator we use the formula twice.
(2) We present similar terms in the numerator.
(3) To eliminate uncertainty, divide the numerator and denominator by (“en” to the highest degree).
As you can see, nothing complicated.
Example 4
Find the limit of the sequence ![]()
This is an example for you to solve on your own, abbreviated multiplication formulas to help.
Within s indicative Sequences use a similar method of dividing the numerator and denominator:
Example 5
Find the limit of the sequence ![]()
Solution Let's arrange it according to the same scheme:
A similar theorem is true, by the way, for functions: the product of a bounded function and an infinitesimal function is an infinitesimal function.
Example 9
Find the limit of the sequence
Mathematics is the science that builds the world. Both the scientist and the common man - no one can do without it. First, young children are taught to count, then to add, subtract, multiply and divide, to high school Letter designations come into play, and in the older game you can’t do without them.
But today we will talk about what all known mathematics is based on. About a community of numbers called “sequence limits”.
What are sequences and where is their limit?
The meaning of the word “sequence” is not difficult to interpret. This is an arrangement of things where someone or something is located in a certain order or queue. For example, the queue for tickets to the zoo is a sequence. And there can only be one! If, for example, you look at the queue at the store, this is one sequence. And if one person from this queue suddenly leaves, then this is a different queue, a different order.
The word “limit” is also easily interpreted - it is the end of something. However, in mathematics, the limits of sequences are those values on the number line to which a sequence of numbers tends. Why does it strive and not end? It's simple, the number line has no end, and most sequences, like rays, have only a beginning and look like this:
x 1, x 2, x 3,...x n...
Hence the definition of a sequence is a function of the natural argument. More in simple words is a series of members of a certain set.
How is the number sequence constructed?
A simple example of a number sequence might look like this: 1, 2, 3, 4, …n…
In most cases, for practical purposes, sequences are built from numbers, and each next member of the series, let's denote it X, has its own name. For example:
x 1 is the first member of the sequence;
x 2 is the second term of the sequence;
x 3 is the third term;
x n is the nth term.
IN practical methods the sequence is given general formula, in which there is some variable. For example:
X n =3n, then the series of numbers itself will look like this:
It is worth remembering that when writing sequences in general, you can use any Latin letters, not just X. For example: y, z, k, etc.
Arithmetic progression as part of sequences
Before looking for the limits of sequences, it is advisable to plunge deeper into the very concept of such a number series, which everyone encountered when they were in middle school. An arithmetic progression is a series of numbers in which the difference between adjacent terms is constant.
Problem: “Let a 1 = 15, and the progression step of the number series d = 4. Construct the first 4 terms of this series"
Solution: a 1 = 15 (by condition) is the first term of the progression (number series).
and 2 = 15+4=19 is the second term of the progression.
and 3 =19+4=23 is the third term.
and 4 =23+4=27 is the fourth term.
However, using this method it is difficult to reach large values, for example up to a 125. . Especially for such cases, a formula convenient for practice was derived: a n =a 1 +d(n-1). In this case, a 125 =15+4(125-1)=511.
Types of sequences
Most of the sequences are endless, it's worth remembering for the rest of your life. There are two interesting looking number series. The first is given by the formula a n =(-1) n. Mathematicians often call this sequence a flasher. Why? Let's check its number series.
1, 1, -1, 1, -1, 1, etc. With an example like this, it becomes clear that numbers in sequences can easily be repeated.
Factorial sequence. It's easy to guess - the formula defining the sequence contains a factorial. For example: a n = (n+1)!
Then the sequence will look like this:
a 2 = 1x2x3 = 6;
and 3 = 1x2x3x4 = 24, etc.
A sequence defined by an arithmetic progression is called infinitely decreasing if the inequality -1 is satisfied for all its terms and 3 = - 1/8, etc. There is even a sequence consisting of the same number. So, n =6 consists of an infinite number of sixes. Sequence limits have long existed in mathematics. Of course, they deserve their own competent design. So, time to learn the definition of sequence limits. First, let's look at the limit for a linear function in detail: It is easy to understand that the definition of the limit of a sequence can be formulated as follows: this is a certain number to which all members of the sequence infinitely approach. A simple example: a x = 4x+1. Then the sequence itself will look like this. 5, 9, 13, 17, 21…x… Thus, this sequence will increase indefinitely, which means its limit is equal to infinity as x→∞, and it should be written like this: If we take a similar sequence, but x tends to 1, we get: And the series of numbers will be like this: 1.4, 1.8, 4.6, 4.944, etc. Each time you need to substitute the number closer to one (0.1, 0.2, 0.9, 0.986). From this series it is clear that the limit of the function is five. From this part it is worth remembering what the limit of a numerical sequence is, the definition and method for solving simple problems. Having examined the limit of a number sequence, its definition and examples, you can proceed to a more complex topic. Absolutely all limits of sequences can be formulated by one formula, which is usually analyzed in the first semester. So, what does this set of letters, modules and inequality signs mean? ∀ is a universal quantifier, replacing the phrases “for all”, “for everything”, etc. ∃ is an existential quantifier, in this case it means that there is some value N belonging to the set of natural numbers. A long vertical stick following N means that the given set N is “such that.” In practice, it can mean “such that”, “such that”, etc. To reinforce the material, read the formula out loud. The method of finding the limit of sequences, which was discussed above, although simple to use, is not so rational in practice. Try to find the limit for this function: If we substitute different values of “x” (increasing each time: 10, 100, 1000, etc.), then we get ∞ in the numerator, but also ∞ in the denominator. This results in a rather strange fraction: But is this really so? Calculating the limit of a number sequence in this case seems quite easy. It would be possible to leave everything as it is, because the answer is ready, and it was received under reasonable conditions, but there is another way specifically for such cases. First, let's find the highest degree in the numerator of the fraction - this is 1, since x can be represented as x 1. Now let's find the highest degree in the denominator. Also 1. Let's divide both the numerator and the denominator by the variable to the highest degree. In this case, divide the fraction by x 1. Next, we will find what value each term containing a variable tends to. In this case, fractions are considered. As x→∞, the value of each fraction tends to zero. When submitting your work in writing, you should make the following footnotes: This results in the following expression: Of course, the fractions containing x did not become zeros! But their value is so small that it is completely permissible not to take it into account in calculations. In fact, x will never be equal to 0 in this case, because you cannot divide by zero. Suppose the professor has at his disposal a complex sequence, given, obviously, by an equally complex formula. The professor has found the answer, but is it right? After all, all people make mistakes. Auguste Cauchy once came up with an excellent way to prove the limits of sequences. His method was called neighborhood manipulation. Suppose that there is a certain point a, its neighborhood in both directions on the number line is equal to ε (“epsilon”). Since the last variable is distance, its value is always positive. Now let's define some sequence x n and assume that the tenth term of the sequence (x 10) is included in the neighborhood of a. How can we write this fact in mathematical language? Let's say x 10 is to the right of point a, then the distance x 10 -a<ε, однако, если расположить «икс десятое» левее точки а, то расстояние получится отрицательным, а это невозможно, значит, следует занести левую часть неравенства под модуль. Получится |х 10 -а|<ε. Now it’s time to explain in practice the formula discussed above. It is fair to call a certain number a the end point of a sequence if for any of its limits the inequality ε>0 is satisfied, and the entire neighborhood has its own natural number N, such that all members of the sequence with higher numbers will be inside the sequence |x n - a|< ε. With such knowledge it is easy to solve the sequence limits, prove or disprove the ready-made answer. Theorems on the limits of sequences are an important component of the theory, without which practice is impossible. There are only four main theorems, remembering which can make the solution or proof much easier: Sometimes you need to solve an inverse problem, to prove a given limit of a numerical sequence. Let's look at an example. Prove that the limit of the sequence given by the formula is zero. According to the rule discussed above, for any sequence the inequality |x n - a|<ε. Подставим заданное значение и точку отсчёта. Получим: Let us express n through “epsilon” to show the existence of a certain number and prove the presence of a limit of the sequence. At this point, it is important to remember that “epsilon” and “en” are positive numbers and are not equal to zero. Now it is possible to continue further transformations using the knowledge about inequalities gained in high school. How does it turn out that n > -3 + 1/ε. Since it is worth remembering that we are talking about natural numbers, the result can be rounded by putting it in square brackets. Thus, it was proven that for any value of the “epsilon” neighborhood of the point a = 0, a value was found such that the initial inequality is satisfied. From here we can safely say that the number a is the limit of a given sequence. Q.E.D. This convenient method can be used to prove the limit of a numerical sequence, no matter how complex it may be at first glance. The main thing is not to panic when you see the task. The existence of a consistency limit is not necessary in practice. You can easily come across series of numbers that really have no end. For example, the same “flashing light” x n = (-1) n. it is obvious that a sequence consisting of only two digits, repeated cyclically, cannot have a limit. The same story is repeated with sequences consisting of one number, fractional ones, having uncertainty of any order during calculations (0/0, ∞/∞, ∞/0, etc.). However, it should be remembered that incorrect calculations also occur. Sometimes double-checking your own solution will help you find the sequence limit. Several examples of sequences and methods for solving them were discussed above, and now let’s try to take a more specific case and call it a “monotonic sequence.” Definition: any sequence can rightly be called monotonically increasing if the strict inequality x n holds for it< x n +1. Также любую последовательность справедливо называть монотонной убывающей, если для неё выполняется неравенство x n >x n +1. Along with these two conditions, there are also similar non-strict inequalities. Accordingly, x n ≤ x n +1 (non-decreasing sequence) and x n ≥ x n +1 (non-increasing sequence). But it’s easier to understand this with examples. The sequence given by the formula x n = 2+n forms the following series of numbers: 4, 5, 6, etc. This is a monotonically increasing sequence. And if we take x n =1/n, we get the series: 1/3, ¼, 1/5, etc. This is a monotonically decreasing sequence. A bounded sequence is a sequence that has a limit. A convergent sequence is a series of numbers that has an infinitesimal limit. Thus, the limit of a bounded sequence is any real or complex number. Remember that there can only be one limit. The limit of a convergent sequence is an infinitesimal (real or complex) quantity. If you draw a sequence diagram, then at a certain point it will seem to converge, tend to turn into a certain value. Hence the name - convergent sequence. There may or may not be a limit to such a sequence. First, it is useful to understand when it exists; from here you can start when proving the absence of a limit. Among monotonic sequences, convergent and divergent are distinguished. Convergent is a sequence that is formed by the set x and has a real or complex limit in this set. Divergent is a sequence that has no limit in its set (neither real nor complex). Moreover, the sequence converges if, in a geometric representation, its upper and lower limits converge. The limit of a convergent sequence can be zero in many cases, since any infinitesimal sequence has a known limit (zero). Whatever convergent sequence you take, they are all bounded, but not all bounded sequences converge. The sum, difference, product of two convergent sequences is also a convergent sequence. However, the quotient can also be convergent if it is defined! Sequence limits are as significant (in most cases) as digits and numbers: 1, 2, 15, 24, 362, etc. It turns out that some operations can be performed with limits. First, like digits and numbers, the limits of any sequence can be added and subtracted. Based on the third theorem on the limits of sequences, the following equality holds: the limit of the sum of sequences is equal to the sum of their limits. Secondly, based on the fourth theorem on the limits of sequences, the following equality is true: the limit of the product of the nth number of sequences is equal to the product of their limits. The same is true for division: the limit of the quotient of two sequences is equal to the quotient of their limits, provided that the limit is not zero. After all, if the limit of sequences is equal to zero, then division by zero will result, which is impossible. It would seem that the limit of the numerical sequence has already been discussed in some detail, but phrases such as “infinitely small” and “infinitely large” numbers are mentioned more than once. Obviously, if there is a sequence 1/x, where x→∞, then such a fraction is infinitesimal, and if the same sequence, but the limit tends to zero (x→0), then the fraction becomes an infinitely large value. And such quantities have their own characteristics. The properties of the limit of a sequence having any small or large values are as follows: In fact, calculating the limit of a sequence is not such a difficult task if you know a simple algorithm. But the limits of consistency are a topic that requires maximum attention and perseverance. Of course, it is enough to simply grasp the essence of the solution to such expressions. Starting small, you can achieve great heights over time.Determining the Sequence Limit



General designation for the limit of sequences

Uncertainty and certainty of the limit





What is a neighborhood?

Theorems
Proof of sequences



Or maybe he's not there?
Monotonic sequence

Limit of a convergent and bounded sequence
Limit of a monotonic sequence
Various actions with limits
Properties of sequence quantities