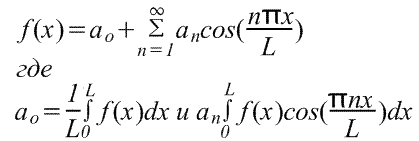Expand the modulus x into a Fourier series. Higher mathematics

Many processes occurring in nature and technology tend to repeat themselves at certain intervals. Such processes are called periodic and are mathematically described by periodic functions. Such functions include sin(x) , cos(x) , sin(wx), cos(wx) . The sum of two periodic functions, for example, a function of the form , generally speaking, is no longer periodic. But it can be proven that if the relation w 1 / w 2 is a rational number, then this sum is a periodic function.

The simplest periodic processes - harmonic oscillations - are described by periodic functions sin(wx) And cos(wx). More complex periodic processes are described by functions composed of either a finite or an infinite number of terms of the form sin(wx) And cos(wx).

3.2. Trigonometric series. Fourier coefficients

Let's consider a functional series of the form:

This series is called trigonometric; numbers A 0 , b 0 , a 1 , b 1 ,A 2 , b 2 …, a n , b n ,… are called coefficients trigonometric series. Series (1) is often written as follows:

. (2)

Since the members of the trigonometric series (2) have a common period
, then the sum of the series, if it converges, is also a periodic function with period
.

Let's assume that the function f(x) is the sum of this series:

. (3)

In this case they say that the function f(x) is expanded into a trigonometric series. Assuming that this series converges uniformly on the interval
, you can determine its coefficients using the formulas:

,
,
. (4)

The coefficients of the series determined by these formulas are called Fourier coefficients.

Trigonometric series (2), the coefficients of which are determined by Fourier formulas (4), are called near Fourier, corresponding to the function f(x).

Thus, if a periodic function f(x) is the sum of a convergent trigonometric series, then this series is its Fourier series.

3.3. Convergence of Fourier series

Formulas (4) show that the Fourier coefficients can be calculated for any integrable on the interval

-periodic function, i.e. For such a function you can always construct a Fourier series. But will this series converge to the function f(x) and under what conditions?

Recall that the function f(x), defined on the segment [ a; b] , is called piecewise smooth if it and its derivative have no more than a finite number of discontinuity points of the first kind.

The following theorem gives sufficient conditions for the decomposability of a function in a Fourier series.

Dirichlet's theorem. Let
-periodic function f(x) is piecewise smooth on
. Then its Fourier series converges to f(x) at each of its points of continuity and to the value 0,5(f(x+0)+ f(x-0)) at the breaking point.

Example 1.

Expand the function into a Fourier series f(x)= x, specified on the interval
.

Solution. This function satisfies the Dirichlet conditions and, therefore, can be expanded in a Fourier series. Using formulas (4) and the method of integration by parts
, we find the Fourier coefficients:

Thus, the Fourier series for the function f(x) has a look.

Fourier series are a representation of an arbitrary function with a specific period in the form of a series. IN general view this decision is called the decomposition of an element in an orthogonal basis. Expansion of functions into Fourier series is a fairly powerful tool for solving various problems due to the properties of this transformation during integration, differentiation, as well as shifting expressions by argument and convolution.

A person who is not familiar with higher mathematics, as well as with the works of the French scientist Fourier, most likely will not understand what these “series” are and what they are needed for. Meanwhile, this transformation has become quite integrated into our lives. It is used not only by mathematicians, but also by physicists, chemists, doctors, astronomers, seismologists, oceanographers and many others. Let us also take a closer look at the works of the great French scientist who made a discovery that was ahead of its time.

Man and the Fourier transform

Fourier series are one of the methods (along with analysis and others). This process occurs every time a person hears a sound. Our ear automatically carries out the transformation elementary particles in an elastic medium are laid out in rows (along the spectrum) of successive loudness level values ​​for tones of different heights. Next, the brain turns this data into sounds that are familiar to us. All this happens without our desire or consciousness, on its own, but in order to understand these processes, it will take several years to study higher mathematics.

More about Fourier transform

The Fourier transform can be carried out using analytical, numerical and other methods. Fourier series refer to the numerical method of decomposing any oscillatory processes - from ocean tides and light waves to cycles of solar (and other astronomical objects) activity. Using these mathematical techniques, you can analyze functions, representing any oscillatory processes as a series of sinusoidal components that move from minimum to maximum and back. The Fourier transform is a function that describes the phase and amplitude of sinusoids corresponding to a specific frequency. This process can be used to solve very complex equations, which describe dynamic processes arising under the influence of thermal, light or electrical energy. Also, Fourier series make it possible to isolate constant components in complex oscillatory signals, making it possible to correctly interpret the experimental observations obtained in medicine, chemistry and astronomy.

Historical reference

The founding father of this theory is the French mathematician Jean Baptiste Joseph Fourier. This transformation was subsequently named after him. Initially, the scientist used his method to study and explain the mechanisms of thermal conductivity - the spread of heat in solids. Fourier suggested that the initial irregular distribution can be decomposed into simple sinusoids, each of which will have its own temperature minimum and maximum, as well as its phase. In this case, each such component will be measured from minimum to maximum and back. The mathematical function that describes the upper and lower peaks of the curve, as well as the phase of each of the harmonics, is called the Fourier transform of the temperature distribution expression. The author of the theory brought together general function distribution, which is difficult to describe mathematically, to a very convenient series of cosine and sine, which together give the original distribution.

The principle of transformation and the views of contemporaries

The scientist's contemporaries - leading mathematicians of the early nineteenth century - did not accept this theory. The main objection was Fourier's assertion that a discontinuous function, describing a straight line or a discontinuous curve, can be represented as a sum of sinusoidal expressions that are continuous. As an example, consider the Heaviside step: its value is zero to the left of the discontinuity and one to the right. This function describes the dependence of electric current on a time variable when a circuit is closed. Contemporaries of the theory at that time had never encountered a similar situation where a discontinuous expression would be described by a combination of continuous, ordinary functions such as exponential, sine, linear or quadratic.

What confused French mathematicians about Fourier's theory?

After all, if the mathematician was right in his statements, then by summing the infinite trigonometric Fourier series, one can obtain an accurate representation of the step expression even if it has many similar steps. At the beginning of the nineteenth century, such a statement seemed absurd. But despite all the doubts, many mathematicians expanded the scope of study of this phenomenon, taking it beyond the study of thermal conductivity. However, most scientists continued to be tormented by the question: “Can the sum of a sinusoidal series converge to exact value discontinuous function?

Convergence of Fourier series: an example

The question of convergence arises whenever it is necessary to sum infinite series of numbers. To understand this phenomenon, consider a classic example. Will you ever be able to reach the wall if each subsequent step is half the size of the previous one? Let's say you're two meters from your target, the first step takes you to the halfway mark, the next one takes you to the three-quarters mark, and after the fifth you'll have covered almost 97 percent of the way. However, no matter how many steps you take, you will not achieve your intended goal in a strict mathematical sense. Using numerical calculations, it can be proven that it is eventually possible to get as close as a given distance. This proof is equivalent to demonstrating that the sum of one-half, one-fourth, etc. will tend to unity.

The Question of Convergence: The Second Coming, or Lord Kelvin's Device

This issue was raised again at the end of the nineteenth century, when they tried to use Fourier series to predict the intensity of tides. At this time, Lord Kelvin invented an instrument, which was an analogue computing device that allowed military and merchant marine sailors to track this a natural phenomenon. This mechanism determined sets of phases and amplitudes from a table of tide heights and corresponding time points, carefully measured in a given harbor throughout the year. Each parameter was a sinusoidal component of the tide height expression and was one of the regular components. The results of the measurements were entered into Lord Kelvin's calculating instrument, which synthesized a curve that predicted the height of the water as a function of time over next year. Very soon similar curves were drawn up for all the harbors of the world.

What if the process is disrupted by a discontinuous function?

At that time it seemed obvious that a tidal wave prediction instrument with big amount account elements can calculate a large number of phases and amplitudes and so provide more accurate predictions. However, it turned out that this pattern is not observed in cases where the tidal expression that should be synthesized contained a sharp jump, that is, it was discontinuous. If data from a table of time moments is entered into the device, it calculates several Fourier coefficients. The original function is restored thanks to the sinusoidal components (in accordance with the found coefficients). The discrepancy between the original and reconstructed expression can be measured at any point. When carrying out repeated calculations and comparisons, it is clear that the value of the largest error does not decrease. However, they are localized in the region corresponding to the discontinuity point, and at any other point they tend to zero. In 1899, this result was theoretically confirmed by Joshua Willard Gibbs of Yale University.

Convergence of Fourier series and the development of mathematics in general

Fourier analysis is not applicable to expressions containing an infinite number of spikes over a certain interval. In general, Fourier series, if the original function is represented by the result of the real physical dimension, always converge. Convergence issues this process for specific classes of functions led to the emergence of new branches in mathematics, for example, the theory of generalized functions. She is associated with such names as L. Schwartz, J. Mikusinski and J. Temple. Within the framework of this theory, a clear and precise theoretical basis under such expressions as the Dirac delta function (it describes a region of a single area concentrated in an infinitesimal neighborhood of a point) and the Heaviside “step”. Thanks to this work, Fourier series became applicable to solving equations and problems involving intuitive concepts: point charge, point mass, magnetic dipoles, and concentrated load on a beam.

Fourier method

Fourier series, in accordance with the principles of interference, begin with the decomposition of complex forms into simpler ones. For example, a change in heat flow is explained by its passage through various obstacles made of heat-insulating material irregular shape or a change in the surface of the earth - an earthquake, a change in the orbit of a celestial body - the influence of planets. As a rule, such equations that describe simple classical systems can be easily solved for each individual wave. Fourier showed that simple solutions can also be summed to obtain solutions to more complex problems. In mathematical terms, Fourier series are a technique for representing an expression as a sum of harmonics - cosine and sine. That's why this analysis also known as harmonic analysis.

Fourier series - an ideal technique before the “computer age”

Before creation computer equipment Fourier's technique was best weapon in the arsenal of scientists when working with the wave nature of our world. The Fourier series in complex form makes it possible to solve not only simple tasks, which are amenable to the direct application of Newton's laws of mechanics, but also fundamental equations. Most of the discoveries of Newtonian science in the nineteenth century were made possible only by Fourier's technique.

Fourier series today

With the development of computers, Fourier transforms have risen to a qualitative level new level. This technique is firmly established in almost all areas of science and technology. An example is digital audio and video. Its implementation became possible only thanks to a theory developed by a French mathematician at the beginning of the nineteenth century. Thus, the Fourier series in complex form made it possible to make a breakthrough in the study outer space. In addition, it influenced the study of the physics of semiconductor materials and plasma, microwave acoustics, oceanography, radar, and seismology.

Trigonometric Fourier series

In mathematics, a Fourier series is a way of representing arbitrary complex functions the sum of simpler ones. IN general cases the number of such expressions can be infinite. Moreover, the more their number is taken into account in the calculation, the more accurate it is. final result. Most often used as protozoa trigonometric functions cosine or sine. In this case, Fourier series are called trigonometric, and the solution of such expressions is called harmonic expansion. This method plays important role in mathematics. First of all, the trigonometric series provides a means for depicting and also studying functions; it is the main apparatus of the theory. In addition, it allows you to solve a number of problems in mathematical physics. Finally, this theory contributed to the development of a number of very important branches of mathematical science (the theory of integrals, the theory of periodic functions). In addition, it served as the starting point for the development of the following functions of a real variable, and also laid the foundation for harmonic analysis.

The Fourier series of an even periodic function f(x) with period 2p contains only terms with cosines (i.e., does not contain terms with sines) and may include a constant term. Hence,

where are the coefficients Fourier series,

Fourier series expansion in sines

The Fourier series of an odd periodic function f (x) with period 2p contains only terms with sines (that is, it does not contain terms with cosines).

Hence,

where are the coefficients of the Fourier series,

Fourier series at half cycle

If a function is defined for a range, say from 0 to p, and not just from 0 to 2p, it can be expanded into a series only in sines or only in cosines. The resulting Fourier series is called near Fourier on half-cycle

If you want to get the decomposition Fourier on half cycle By cosines functions f (x) in the range from 0 to p, then it is necessary to construct an even periodic function. In Fig. Below is the function f (x) = x, built on the interval from x = 0 to x = p. Since the even function is symmetrical about the f (x) axis, we draw line AB, as shown in Fig. below. If we assume that outside the considered interval the obtained triangular shape is periodic with a period of 2p, then the final graph looks like, show. in Fig. below. Since we need to obtain the Fourier expansion in cosines, as before, we calculate the Fourier coefficients a o and a n

If you need to get decomposition Fourier on half cycle By sinuses functions f (x) in the range from 0 to p, then it is necessary to construct an odd periodic function. In Fig. Below is the function f (x) =x, built on the interval from x=0 to x=p. Since the odd function is symmetrical about the origin, we construct the line CD, as shown in Fig.

If we assume that outside the considered interval the resulting sawtooth signal is periodic with a period of 2p, then the final graph has the form shown in Fig. Since we need to obtain the Fourier expansion of the half-cycle in terms of sines, as before, we calculate the Fourier coefficient. b

Ministry of General and Vocational Education

Sochi State University tourism

and resort business

Pedagogical Institute

Faculty of Mathematics

Department of General Mathematics

GRADUATE WORK

Fourier series and their applications

In mathematical physics.

Completed by: 5th year student

signature of full-time education

Specialty 010100

"Mathematics"

Kasperova N.S.

Student ID No. 95471

Scientific supervisor: associate professor, candidate.

technical signature sciences

Pozin P.A.

Sochi, 2000

1. Introduction.

2. The concept of a Fourier series.

2.1. Determination of Fourier series coefficients.

2.2. Integrals of periodic functions.

3. Signs of convergence of Fourier series.

3.1. Examples of expansion of functions in Fourier series.

4. A note on the Fourier series expansion of a periodic function

5. Fourier series for even and odd functions.

6. Fourier series for functions with period 2 l .

7. Fourier series expansion of a non-periodic function.

Introduction.

Jean Baptiste Joseph Fourier - French mathematician, member of the Paris Academy of Sciences (1817).

Fourier's first works related to algebra. Already in lectures of 1796 he expounded the theorem on the number real roots algebraic equation lying between these borders (published 1820), named after him; a complete solution to the number of real roots of an algebraic equation was obtained in 1829 by J.S.F. By assault. In 1818, Fourier investigated the question of the conditions for the applicability of the method of numerical solution of equations developed by Newton, not knowing about similar results obtained in 1768 by the French mathematician J.R. Murailem. The result of Fourier’s work on numerical methods for solving equations is “Analysis certain equations", published posthumously in 1831.

Fourier's main area of ​​study was mathematical physics. In 1807 and 1811 he presented to the Paris Academy of Sciences his first discoveries on the theory of heat propagation in solid body, and in 1822 published famous work « Analytical theory heat", which played a major role in the subsequent history of mathematics. This - mathematical theory thermal conductivity. Due to the generality of the method, this book became the source of all modern methods mathematical physics. In this work, Fourier derived differential equation thermal conductivity and developed ideas in the most general outline outlined earlier by D. Bernoulli, developed a method for separating variables (Fourier method) to solve the heat equation under certain given boundary conditions, which he applied to a number of special cases (cube, cylinder, etc.). This method is based on the representation of functions by trigonometric Fourier series.

Fourier series have now become a well-developed tool in the theory of partial differential equations for solving boundary value problems.

1. The concept of a Fourier series.(p. 94, Uvarenkov)

Fourier series play an important role in mathematical physics, elasticity theory, electrical engineering, and especially their special case - trigonometric Fourier series.

A trigonometric series is a series of the form

or, symbolically:

(1)

where ω, a 0, a 1, …, a n, …, b 0, b 1, …, b n, … are constant numbers (ω>0).

Historically, certain problems in physics have led to the study of such series, for example, the problem of string vibrations (18th century), the problem of regularities in the phenomena of heat conduction, etc. In applications, consideration of trigonometric series , is primarily associated with the task of representing a given movement, described by the equation y = ƒ(χ), in

in the form of a sum of the simplest harmonic oscillations, often taken in an infinitely large number, i.e., as the sum of a series of the form (1).

Thus, we come to the following problem: to find out whether for a given function ƒ(x) on a given interval there exists a series (1) that would converge on this interval to this function. If this is possible, then they say that on this interval the function ƒ(x) is expanded into a trigonometric series.

Series (1) converges at some point x 0, due to the periodicity of the functions

(n=1,2,..), it will turn out to be convergent at all points of the form (m is any integer), and thus its sum S(x) will be (in the region of convergence of the series) a periodic function: if S n ( x) is the nth partial sum of this series, then we have

and therefore

, i.e. S(x 0 +T)=S(x 0). Therefore, speaking about the expansion of some function ƒ(x) into a series of the form (1), we will assume ƒ(x) to be a periodic function.

2. Determination of series coefficients using Fourier formulas.

Let a periodic function ƒ(x) with period 2π be such that it is represented by a trigonometric series converging to a given function in the interval (-π, π), i.e., is the sum of this series:

. (2)

Let us assume that the integral of the function on the left side of this equality is equal to the sum of the integrals of the terms of this series. This will be true if we assume that the number series composed of the coefficients of a given trigonometric series is absolutely convergent, i.e., the positive number series converges

(3)

Series (1) is majorizable and can be integrated term by term in the interval (-π, π). Let's integrate both sides of equality (2):

.

Let us separately evaluate each integral appearing on the right-hand side:

, , .

Thus,

, where . (4)

Estimation of Fourier coefficients.(Bugrov)

Theorem 1. Let the function ƒ(x) of period 2π have a continuous derivative ƒ ( s) (x) order s, satisfying the inequality on the entire real axis:

│ ƒ (s) (x)│≤ M s ; (5)

then the Fourier coefficients of the function ƒ satisfy the inequality

(6)

Proof. Integrating by parts and taking into account that

ƒ(-π) = ƒ(π), we have

Integrating right side(7) consistently, taking into account that the derivatives ƒ ΄, …, ƒ (s-1) are continuous and take same values at points t = -π and t = π, as well as estimate (5), we obtain the first estimate (6).

The second estimate (6) is obtained in a similar way.

Theorem 2. For the Fourier coefficients ƒ(x) the following inequality holds:

(8)

Proof. We have

Fourier series of periodic functions with period 2π.

The Fourier series allows us to study periodic functions by decomposing them into components. Alternating currents and voltages, displacements, speed and acceleration of crank mechanisms and acoustic waves are typical practical examples application of periodic functions in engineering calculations.

Fourier series expansion is based on the assumption that all having practical significance functions in the interval -π ≤x≤ π can be expressed in the form of convergent trigonometric series (a series is considered convergent if the sequence of partial sums composed of its terms converges):

Standard (=ordinary) notation through the sum of sinx and cosx

f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,

where a o, a 1,a 2,...,b 1,b 2,.. are real constants, i.e.

Where, for the range from -π to π, the coefficients of the Fourier series are calculated using the formulas:

The coefficients a o , a n and b n are called Fourier coefficients, and if they can be found, then series (1) is called next to Fourier, corresponding to the function f(x). For series (1), the term (a 1 cosx+b 1 sinx) is called the first or fundamental harmonic,

Another way to write a series is to use the relation acosx+bsinx=csin(x+α)

f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)

Where a o is a constant, c 1 =(a 1 2 +b 1 2) 1/2, c n =(a n 2 +b n 2) 1/2 are the amplitudes of the various components, and is equal to a n =arctg a n /b n.

For series (1), the term (a 1 cosx+b 1 sinx) or c 1 sin(x+α 1) is called the first or fundamental harmonic,(a 2 cos2x+b 2 sin2x) or c 2 sin(2x+α 2) is called second harmonic and so on.

To accurately represent a complex signal typically requires an infinite number of terms. However, in many practical problems it is sufficient to consider only the first few terms.

Fourier series of non-periodic functions with period 2π.

Expansion of non-periodic functions.

If the function f(x) is non-periodic, it means that it cannot be expanded into a Fourier series for all values ​​of x. However, it is possible to define a Fourier series representing a function over any range of width 2π.

Given a non-periodic function, a new function can be constructed by selecting values ​​of f(x) within a certain range and repeating them outside that range at 2π intervals. Since the new function is periodic with period 2π, it can be expanded into a Fourier series for all values ​​of x. For example, the function f(x)=x is not periodic. However, if it is necessary to expand it into a Fourier series in the interval from o to 2π, then outside this interval a periodic function with a period of 2π is constructed (as shown in the figure below).

For non-periodic functions such as f(x)=x, the sum of the Fourier series is equal to the value of f(x) at all points in a given range, but it is not equal to f(x) for points outside the range. To find the Fourier series of a non-periodic function in the 2π range, the same formula of Fourier coefficients is used.

Even and odd functions.

They say the function y=f(x) even, if f(-x)=f(x) for all values ​​of x. Graphs of even functions are always symmetrical about the y-axis (that is, they are mirror images). Two examples of even functions: y=x2 and y=cosx.

They say that the function y=f(x) odd, if f(-x)=-f(x) for all values ​​of x. Graphs of odd functions are always symmetrical about the origin.

Many functions are neither even nor odd.

Fourier series expansion in cosines.

The Fourier series of an even periodic function f(x) with period 2π contains only cosine terms (i.e., no sine terms) and may include a constant term. Hence,

where are the coefficients of the Fourier series,

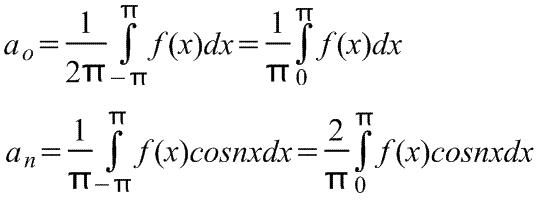
The Fourier series of an odd periodic function f(x) with period 2π contains only terms with sines (that is, it does not contain terms with cosines).

Hence,

where are the coefficients of the Fourier series,

Fourier series at half cycle.

If a function is defined for a range, say from 0 to π, and not just from 0 to 2π, it can be expanded in a series only in sines or only in cosines. The resulting Fourier series is called near Fourier at half cycle.

If you want to get the decomposition Half-cycle Fourier by cosines functions f(x) in the range from 0 to π, then it is necessary to construct an even periodic function. In Fig. Below is the function f(x)=x, built on the interval from x=0 to x=π. Since the even function is symmetrical about the f(x) axis, we draw line AB, as shown in Fig. below. If we assume that outside the considered interval the resulting triangular shape is periodic with a period of 2π, then the final graph looks like this: in Fig. below. Since we need to obtain the Fourier expansion in cosines, as before, we calculate the Fourier coefficients a o and a n

If you need to get Fourier half-cycle sine expansion functions f(x) in the range from 0 to π, then it is necessary to construct an odd periodic function. In Fig. Below is the function f(x)=x, built on the interval from x=0 to x=π. Since the odd function is symmetrical about the origin, we construct the line CD, as shown in Fig. If we assume that outside the considered interval the resulting sawtooth signal is periodic with a period of 2π, then the final graph has the form shown in Fig. Since we need to obtain the Fourier expansion of the half-cycle in terms of sines, as before, we calculate the Fourier coefficient. b

Fourier series for an arbitrary interval.

Expansion of a periodic function with period L.

The periodic function f(x) repeats as x increases by L, i.e. f(x+L)=f(x). The transition from the previously considered functions with a period of 2π to functions with a period of L is quite simple, since it can be done using a change of variable.

To find the Fourier series of the function f(x) in the range -L/2≤x≤L/2, we introduce a new variable u so that the function f(x) has a period of 2π relative to u. If u=2πx/L, then x=-L/2 for u=-π and x=L/2 for u=π. Also let f(x)=f(Lu/2π)=F(u). The Fourier series F(u) has the form

(The limits of integration can be replaced by any interval of length L, for example, from 0 to L)

Fourier series on a half-cycle for functions specified in the interval L≠2π.

For the substitution u=πх/L, the interval from x=0 to x=L corresponds to the interval from u=0 to u=π. Consequently, the function can be expanded into a series only in cosines or only in sines, i.e. V Fourier series at half cycle.

The cosine expansion in the range from 0 to L has the form