Kalkulator untuk menyelesaikan sistem pertidaksamaan. Sistem pertidaksamaan linier

Sistem ketidaksetaraan.
Contoh 1. Temukan domain suatu ekspresi
Larutan. Di bawah tanda akar kuadrat seharusnya tidak ada angka negatif, yang berarti dua pertidaksamaan harus dipenuhi secara bersamaan: Dalam kasus seperti ini, mereka mengatakan bahwa permasalahannya adalah menyelesaikan sistem kesenjangan

Namun kita belum menemukan model matematika (sistem pertidaksamaan) seperti itu. Artinya, kita belum dapat menyelesaikan solusi dari contoh tersebut.

Pertidaksamaan yang membentuk suatu sistem digabungkan dengan tanda kurung kurawal (hal yang sama juga berlaku dalam sistem persamaan). Misalnya, rekam

artinya pertidaksamaan 2x - 1 > 3 dan 3x - 2< 11 образуют систему неравенств.

Terkadang sistem pertidaksamaan ditulis dalam bentuk pertidaksamaan ganda. Misalnya saja sistem ketimpangan

dapat ditulis sebagai pertidaksamaan ganda 3<2х-1<11.

Dalam kursus aljabar kelas 9, kita hanya akan membahas sistem dua pertidaksamaan.

Pertimbangkan sistem ketidaksetaraan

Anda dapat memilih beberapa solusi khususnya, misalnya x = 3, x = 4, x = 3.5. Faktanya, untuk x = 3 pertidaksamaan pertama berbentuk 5 > 3, dan pertidaksamaan kedua berbentuk 7< 11. Получились два верных числовых неравенства, значит, х = 3 - решение системы неравенств. Точно так же можно убедиться в том, что х = 4, х = 3,5 - решения системы неравенств.

Pada saat yang sama, nilai x = 5 bukanlah solusi sistem pertidaksamaan. Jika x = 5, pertidaksamaan pertama berbentuk 9 > 3 - pertidaksamaan numerik benar, dan pertidaksamaan kedua berbentuk 13< 11- неверное числовое неравенство .
Menyelesaikan sistem pertidaksamaan berarti menemukan semua solusi khusus dari sistem tersebut. Jelas bahwa tebakan di atas bukanlah metode untuk menyelesaikan sistem pertidaksamaan. DI DALAM contoh berikut Kami akan menunjukkan bagaimana orang biasanya bernalar ketika menyelesaikan sistem ketidaksetaraan.

Contoh 3. Selesaikan sistem pertidaksamaan:

Larutan.

A) Menyelesaikan pertidaksamaan pertama sistem, kita menemukan 2x > 4, x > 2; menyelesaikan pertidaksamaan kedua dari sistem, kita menemukan 3x< 13 Отметим эти промежутки на одной координатной прямой , использовав для выделения первого промежутка верхнюю штриховку, а для второго - нижнюю штриховку (рис. 22). Решением системы неравенств будет пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали. В рассматриваемом примере получаем интервал
B) Menyelesaikan pertidaksamaan pertama sistem, kita menemukan x > 2; menyelesaikan pertidaksamaan kedua dari sistem, kita temukan Mari kita tandai interval ini pada satu garis koordinat, menggunakan arsiran atas untuk interval pertama, dan arsiran bawah untuk interval kedua (Gbr. 23). Penyelesaian sistem pertidaksamaan adalah perpotongan penyelesaian pertidaksamaan sistem, yaitu. interval di mana kedua palka bertepatan. Dalam contoh yang sedang dipertimbangkan, kita memperoleh balok

V) Memecahkan pertidaksamaan pertama sistem, kita menemukan x< 2; решая второе неравенство системы, находим Отметим эти промежутки на одной координатной прямой, использовав для первого промежутка верхнюю штриховку, а для второго - нижнюю штриховку (рис. 24). Решением системы неравенств будет пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали. Здесь такого промежутка нет, значит, система неравенств не имеет решений.

Mari kita menggeneralisasi alasan yang diberikan dalam contoh yang dipertimbangkan. Misalkan kita perlu menyelesaikan sistem pertidaksamaan

Misalkan interval (a, b) merupakan penyelesaian pertidaksamaan fx 2 > g(x), dan interval (c, d) merupakan penyelesaian pertidaksamaan f 2 (x) > s 2 (x ). Mari kita tandai interval ini pada satu garis koordinat, menggunakan arsiran atas untuk interval pertama, dan arsiran bawah untuk interval kedua (Gbr. 25). Penyelesaian sistem pertidaksamaan adalah perpotongan penyelesaian pertidaksamaan sistem tersebut, yaitu. interval di mana kedua palka bertepatan. Pada Gambar. 25 adalah interval (c, b).

Sekarang kita tanpanya tenaga kerja khusus kita dapat menyelesaikan sistem pertidaksamaan yang kita peroleh di atas pada contoh 1:

Menyelesaikan pertidaksamaan pertama sistem, kita menemukan x > 2; menyelesaikan pertidaksamaan kedua dari sistem, kita menemukan x< 8. Отметим эти промежутки (лучи) на одной координатной прямой, использовав для первого -верхнюю, а для второго - нижнюю штриховку (рис. 26). Решением системы неравенств будет пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали, - отрезок . Это - область определения того выражения, о котором шла речь в примере 1.

Tentu saja, sistem ketimpangan tidak harus selalu berupa ketimpangan linier, seperti yang terjadi selama ini; Ketimpangan rasional apa pun (dan bukan hanya rasional) bisa saja terjadi. Secara teknis, menangani sistem pertidaksamaan nonlinier rasional tentu saja lebih rumit, tetapi tidak ada hal baru yang mendasar di sini (dibandingkan dengan sistem pertidaksamaan linier).

Contoh 4. Memecahkan sistem kesenjangan

Larutan.

1) Selesaikan pertidaksamaan yang kita miliki
Mari kita tandai titik -3 dan 3 pada garis bilangan (Gbr. 27). Mereka membagi garis menjadi tiga interval, dan pada setiap interval ekspresi p(x) = (x- 3)(x + 3) mempertahankan tanda konstan - tanda-tanda ini ditunjukkan pada Gambar. 27. Kita tertarik pada interval di mana pertidaksamaan p(x) > 0 berlaku (diarsir pada Gambar 27), dan titik-titik di mana persamaan p(x) = 0 berlaku, yakni titik x = -3, x = 3 (ditandai pada Gambar 2 7 dengan lingkaran hitam). Jadi, pada Gambar. Gambar 27 menyajikan model geometris untuk menyelesaikan pertidaksamaan pertama.

2) Selesaikan pertidaksamaan yang kita miliki
Mari kita tandai titik 0 dan 5 pada garis bilangan (Gbr. 28). Mereka membagi garis menjadi tiga interval, dan pada setiap interval terdapat ekspresi<7(х) = х(5 - х) сохраняет постоянный знак - эти знаки указаны на рис. 28. Нас интересуют промежутки, на которых выполняется неравенство g(х) >O (diarsir pada Gambar 28), dan titik-titik di mana persamaan g (x) - O terpenuhi, yaitu. titik x = 0, x = 5 (ditandai pada Gambar 28 dengan lingkaran hitam). Jadi, pada Gambar. Gambar 28 menyajikan model geometris untuk menyelesaikan pertidaksamaan kedua sistem.

3) Mari kita tandai solusi yang ditemukan untuk pertidaksamaan pertama dan kedua dari sistem pada garis koordinat yang sama, menggunakan arsiran atas untuk penyelesaian pertidaksamaan pertama, dan arsiran bawah untuk penyelesaian pertidaksamaan kedua (Gbr. 29). Penyelesaian sistem pertidaksamaan adalah perpotongan penyelesaian pertidaksamaan sistem, yaitu. interval di mana kedua palka bertepatan. Interval seperti itu adalah sebuah segmen.

Contoh 5. Selesaikan sistem pertidaksamaan:

Larutan:

A) Dari pertidaksamaan pertama kita menemukan x >2. Mari kita perhatikan pertidaksamaan kedua. Trinomial persegi x 2 + x + 2 tidak memiliki akar nyata, dan koefisien utamanya (koefisien pada x 2) adalah positif. Artinya, untuk semua x, pertidaksamaan x 2 + x + 2>0 berlaku, sehingga pertidaksamaan kedua dari sistem tersebut tidak memiliki solusi. Apa dampaknya bagi sistem kesenjangan? Artinya sistem tidak mempunyai solusi.

B) Dari pertidaksamaan pertama kita menemukan x > 2, dan pertidaksamaan kedua dipenuhi untuk sembarang nilai x. Apa dampaknya bagi sistem kesenjangan? Artinya solusinya berbentuk x>2, yaitu. bertepatan dengan penyelesaian pertidaksamaan pertama.

Menjawab:

a) tidak ada solusi; B) x >2.

Contoh ini adalah ilustrasi berguna berikut ini

1. Jika dalam suatu sistem yang memiliki beberapa pertidaksamaan dengan satu variabel, satu pertidaksamaan tidak mempunyai solusi, maka sistem tersebut tidak mempunyai solusi.

2. Jika dalam suatu sistem yang terdiri dari dua pertidaksamaan dengan satu variabel, satu pertidaksamaan terpenuhi untuk sembarang nilai variabel tersebut, maka penyelesaian sistem tersebut adalah penyelesaian pertidaksamaan kedua dari sistem tersebut.

Sebagai penutup bagian ini, mari kita kembali ke soal tentang bilangan yang dimaksudkan yang diberikan di awal dan menyelesaikannya, seperti yang mereka katakan, sesuai dengan semua aturan.

Contoh 2(lihat hal. 29). Disengaja bilangan asli. Diketahui jika kuadrat bilangan yang dituju dijumlahkan 13, maka hasilnya akan lebih besar dari hasil kali bilangan yang dituju dan bilangan 14. Jika dijumlahkan 45 dengan kuadrat dari bilangan yang dituju, maka jumlah tersebut akan menjadi menjadi produk yang lebih sedikit nomor rencana dan nomor 18. Nomor rencana berapa?

Larutan.

Tahap pertama. Menyusun model matematika.
Bilangan x yang dimaksud, seperti kita lihat di atas, harus memenuhi sistem pertidaksamaan

Fase kedua. Bekerja dengan model matematika yang dikompilasi Mari kita ubah pertidaksamaan pertama sistem ke dalam bentuk
x2- 14x+ 13 > 0.

Mari kita cari akar-akar trinomial x 2 - 14x + 13: x 2 = 1, x 2 = 13. Dengan menggunakan parabola y = x 2 - 14x + 13 (Gbr. 30) kita simpulkan bahwa pertidaksamaan yang kita minati adalah puas di x< 1 или x > 13.

Mari kita ubah pertidaksamaan kedua sistem tersebut ke bentuk x2 - 18 2 + 45< 0. Найдем корни трехчлена х 2 - 18x + 45: = 3, х 2 = 15.

Artikel ini memberikan informasi awal tentang sistem kesenjangan. Berikut pengertian sistem pertidaksamaan dan pengertian penyelesaian sistem pertidaksamaan. Jenis sistem utama yang paling sering harus dikerjakan dalam pelajaran aljabar di sekolah juga dicantumkan, dan contohnya diberikan.

Navigasi halaman.

Apa yang dimaksud dengan sistem kesenjangan?

Lebih mudah untuk mendefinisikan sistem pertidaksamaan dengan cara yang sama seperti kita memperkenalkan definisi sistem persamaan, yaitu berdasarkan jenis notasi dan makna yang terkandung di dalamnya.

Definisi.

Sistem ketidaksetaraan adalah catatan yang mewakili sejumlah pertidaksamaan yang ditulis satu di bawah yang lain, disatukan di sebelah kiri dengan tanda kurung kurawal, dan menunjukkan himpunan semua solusi yang sekaligus merupakan solusi untuk setiap pertidaksamaan dalam sistem.

Mari kita beri contoh sistem ketidaksetaraan. Mari kita ambil dua bilangan sembarang, misalnya, 2 x−3>0 dan 5−x≥4 x−11, tuliskan satu di bawah yang lain
2 x−3>0 ,
5−x≥4 x−11
dan disatukan dengan tanda sistem – kurung kurawal, sehingga diperoleh sistem pertidaksamaan berbentuk sebagai berikut:

Gagasan serupa diberikan tentang sistem kesenjangan dalam buku pelajaran sekolah. Perlu dicatat bahwa definisi mereka diberikan lebih sempit: untuk ketidaksetaraan dengan satu variabel atau dengan dua variabel.

Jenis utama sistem ketidaksetaraan

Jelas bahwa kita bisa saja menciptakan banyak sistem kesenjangan yang berbeda-beda. Agar tidak tersesat dalam keberagaman ini, disarankan untuk mempertimbangkan mereka dalam kelompok yang memiliki kelompoknya sendiri fitur. Semua sistem kesenjangan dapat dibagi menjadi beberapa kelompok berdasarkan kriteria berikut:

• berdasarkan jumlah kesenjangan dalam sistem;
• berdasarkan jumlah variabel yang terlibat dalam pencatatan;
• berdasarkan jenis kesenjangan itu sendiri.

Berdasarkan jumlah pertidaksamaan yang termasuk dalam pencatatan, sistem dua, tiga, empat, dst dibedakan. kesenjangan Pada paragraf sebelumnya kita telah memberikan contoh sistem, yaitu sistem dengan dua pertidaksamaan. Mari kita tunjukkan contoh lain dari sistem empat pertidaksamaan .

Secara terpisah, kami akan mengatakan bahwa tidak ada gunanya membicarakan sistem ketidaksetaraan tunggal, dalam hal ini, pada dasarnya yang sedang kita bicarakan tentang ketimpangan itu sendiri, bukan tentang sistemnya.

Jika dilihat dari jumlah variabelnya, maka terdapat sistem pertidaksamaan dengan satu, dua, tiga, dst. variabel (atau, seperti yang juga mereka katakan, tidak diketahui). Lihatlah sistem pertidaksamaan terakhir yang ditulis dua paragraf di atas. Ini adalah sistem dengan tiga variabel x, y dan z. Perlu diingat bahwa dua pertidaksamaan pertamanya tidak memuat ketiga variabel tersebut, melainkan hanya satu saja. Dalam konteks sistem ini, persamaan tersebut harus dipahami sebagai pertidaksamaan dengan tiga variabel yang masing-masing berbentuk x+0·y+0·z≥−2 dan 0·x+y+0·z≤5. Perhatikan bahwa sekolah berfokus pada kesenjangan dengan satu variabel.

Masih perlu dibahas jenis-jenis kesenjangan yang terjadi dalam sistem pencatatan. Di sekolah, mereka terutama mempertimbangkan sistem dua ketidaksetaraan (lebih jarang - tiga, bahkan lebih jarang - empat atau lebih) dengan satu atau dua variabel, dan ketidaksetaraan itu sendiri biasanya seluruh kesenjangan derajat pertama atau kedua (lebih jarang - lebih banyak derajat tinggi atau rasional pecahan). Namun jangan heran jika dalam materi persiapan UN Anda menjumpai sistem pertidaksamaan yang mengandung pertidaksamaan irasional, logaritmik, eksponensial, dan lainnya. Sebagai contoh, kami memberikan sistem ketidaksetaraan , itu diambil dari .

Apa solusi untuk sistem kesenjangan?

Mari kita perkenalkan definisi lain yang berkaitan dengan sistem pertidaksamaan - definisi penyelesaian sistem pertidaksamaan:

Definisi.

Memecahkan sistem pertidaksamaan dengan satu variabel disebut nilai suatu variabel yang mengubah setiap pertidaksamaan sistem menjadi benar, dengan kata lain merupakan penyelesaian setiap pertidaksamaan sistem.

Mari kita jelaskan dengan sebuah contoh. Mari kita ambil sistem dua pertidaksamaan dengan satu variabel. Mari kita ambil nilai variabel x sama dengan 8, ini adalah solusi untuk sistem pertidaksamaan kita menurut definisi, karena substitusinya ke dalam pertidaksamaan sistem menghasilkan dua pertidaksamaan numerik yang benar 8>7 dan 2−3·8≤0. Sebaliknya, kesatuan bukanlah penyelesaian sistem, karena jika disubstitusikan ke variabel x, pertidaksamaan pertama akan berubah menjadi pertidaksamaan numerik salah 1>7.

Demikian pula, seseorang dapat memperkenalkan definisi penyelesaian sistem pertidaksamaan dengan dua, tiga dan jumlah yang besar variabel:

Definisi.

Memecahkan sistem pertidaksamaan dengan dua, tiga, dst. variabel disebut sepasang, tiga, dan seterusnya. nilai-nilai variabel-variabel tersebut, yang sekaligus merupakan penyelesaian setiap pertidaksamaan sistem, yaitu mengubah setiap pertidaksamaan sistem menjadi pertidaksamaan numerik yang benar.

Misalnya sepasang nilai x=1, y=2 atau notasi lain (1, 2) merupakan penyelesaian sistem pertidaksamaan dua variabel, karena 1+2<7 и 1−2<0 - верные числовые неравенства. А пара (3,5, 3) не является решением этой системы, так как второе неравенство при этих значениях переменных дает неверное числовое неравенство 3,5−3<0 .

Sistem pertidaksamaan mungkin tidak mempunyai solusi, mungkin mempunyai jumlah solusi terbatas, atau mungkin mempunyai jumlah solusi tak terhingga. Orang sering berbicara tentang serangkaian solusi terhadap sistem kesenjangan. Jika suatu sistem tidak memiliki solusi, maka terdapat himpunan solusi yang kosong. Jika terdapat solusi yang jumlahnya berhingga, maka himpunan solusi tersebut mengandung elemen yang jumlahnya berhingga, dan jika terdapat banyak solusi yang tak terhingga, maka himpunan solusi tersebut terdiri dari elemen yang jumlahnya tak terhingga.

Beberapa sumber memperkenalkan definisi solusi khusus dan umum untuk sistem ketidaksetaraan, seperti, misalnya, dalam buku teks Mordkovich. Di bawah solusi pribadi dari sistem ketidaksetaraan memahami satu keputusannya. Pada gilirannya solusi umum untuk sistem pertidaksamaan- ini semua adalah keputusan pribadinya. Namun, istilah-istilah ini hanya masuk akal jika perlu untuk secara spesifik menekankan solusi seperti apa yang sedang kita bicarakan, namun biasanya hal ini sudah jelas dari konteksnya, sehingga lebih sering istilah-istilah tersebut hanya mengatakan “solusi terhadap sistem ketidaksetaraan.”

Dari pengertian sistem pertidaksamaan dan penyelesaiannya yang dikemukakan dalam artikel ini, maka penyelesaian sistem pertidaksamaan adalah perpotongan himpunan penyelesaian semua pertidaksamaan sistem tersebut.

Bibliografi.

1. Aljabar: buku pelajaran untuk kelas 8. pendidikan umum institusi / [Yu. N. Makarychev, N.G. Mindyuk, K.I. Neshkov, S.B. Suvorova]; diedit oleh S.A.Telyakovsky. - edisi ke-16. - M.: Pendidikan, 2008. - 271 hal. : sakit. - ISBN 978-5-09-019243-9.
2. Aljabar: kelas 9: mendidik. untuk pendidikan umum institusi / [Yu. N. Makarychev, N.G. Mindyuk, K.I. Neshkov, S.B. Suvorova]; diedit oleh S.A.Telyakovsky. - edisi ke-16. - M.: Pendidikan, 2009. - 271 hal. : sakit. - ISBN 978-5-09-021134-5.
3. Mordkovich A.G. Aljabar. kelas 9. Dalam 2 jam Bagian 1. Buku teks untuk siswa lembaga pendidikan umum / A. G. Mordkovich, P. V. Semenov. - Edisi ke-13, terhapus. - M.: Mnemosyne, 2011. - 222 hal.: sakit. ISBN 978-5-346-01752-3.
4. Mordkovich A.G. Aljabar dan awal analisis matematika. Kelas 11. Dalam 2 jam Bagian 1. Buku teks untuk siswa lembaga pendidikan umum (tingkat profil) / A. G. Mordkovich, P. V. Semenov. - Edisi ke-2, terhapus. - M.: Mnemosyne, 2008. - 287 hal.: sakit. ISBN 978-5-346-01027-2.
5. Ujian Negara Bersatu-2013. Matematika: pilihan ujian standar: 30 pilihan / ed. A.L.Semenova, I.V.Yashchenko. – M.: Penerbitan “Pendidikan Nasional”, 2012. – 192 hal. – (USE-2013. FIPI - sekolah).

Pertidaksamaan adalah dua bilangan atau ekspresi matematika yang dihubungkan oleh salah satu tanda: > (lebih besar dari, dalam kasus pertidaksamaan tegas),< (меньше, в случае строгих неравенств), ≥ (больше или равно, в случае нестрогих неравенств), ≤ (меньше или равно, в случае нестрогих неравенств).

Ketimpangan adalah linier dalam kondisi yang sama dengan persamaan: persamaan hanya memuat variabel sampai derajat pertama dan tidak memuat hasil kali variabel.

Penyelesaian pertidaksamaan linier dan sistem pertidaksamaan linier terkait erat dengan makna geometrisnya: penyelesaian pertidaksamaan linier adalah setengah bidang tertentu yang seluruh bidangnya dibagi oleh sebuah garis lurus, yang persamaannya mendefinisikan pertidaksamaan linier. . Setengah bidang ini, dan dalam kasus sistem pertidaksamaan linier, bagian bidang yang dibatasi oleh beberapa garis lurus, harus ditemukan pada gambar.

Banyak masalah ekonomi, khususnya masalah program linier, yang memerlukan pencarian fungsi maksimum atau minimum, direduksi menjadi penyelesaian sistem pertidaksamaan linier dengan sejumlah besar variabel.

Memecahkan sistem pertidaksamaan linier dengan sejumlah hal yang tidak diketahui

Pertama, mari kita lihat pertidaksamaan linier pada bidang tersebut. Misalkan satu pertidaksamaan dengan dua variabel dan :

,

dimana adalah koefisien dari variabel-variabel (beberapa bilangan), adalah suku bebas (juga suatu bilangan).

Satu pertidaksamaan dengan dua hal yang tidak diketahui, seperti sebuah persamaan, memiliki jumlah penyelesaian yang tak terhingga. Penyelesaian pertidaksamaan ini adalah sepasang bilangan yang memenuhi pertidaksamaan tersebut. Secara geometris, himpunan penyelesaian suatu pertidaksamaan digambarkan sebagai setengah bidang yang dibatasi oleh garis lurus

,

yang akan kita sebut garis batas.

Langkah 1. Buatlah garis yang membatasi himpunan solusi pertidaksamaan linier

Untuk melakukan ini, Anda perlu mengetahui dua titik mana pun pada garis ini. Mari kita cari titik potong dengan sumbu koordinat. Koordinat persimpangan A sama dengan nol (Gambar 1). Nilai numerik pada sumbu pada gambar ini mengacu pada contoh 1, yang akan kita analisis segera setelah perjalanan teoretis ini.

Kita mencari absisnya dengan menyelesaikan persamaan garis dengan persamaan sumbu sebagai suatu sistem.

Mari kita cari perpotongan dengan sumbu:

Mengganti nilai ke dalam persamaan pertama, kita mendapatkan

Di mana .

Jadi, kami menemukan absis intinya A .

Mari kita cari koordinat titik potong dengan sumbunya.

Titik absis B sama dengan nol. Mari kita selesaikan persamaan garis batas dengan persamaan sumbu koordinat:

,

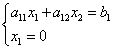
oleh karena itu, koordinat titik tersebut B: .

Langkah 2. Gambarlah garis lurus yang membatasi himpunan solusi pertidaksamaan. Mengetahui poin-poinnya A Dan B perpotongan garis batas dengan sumbu koordinat, kita dapat menggambar garis ini. Sebuah garis lurus (sekali lagi Gambar 1) membagi seluruh bidang menjadi dua bagian yang terletak di kanan dan kiri (atas dan bawah) garis lurus tersebut.

Langkah 3. Tentukan setengah bidang manakah yang merupakan solusi dari pertidaksamaan ini. Untuk melakukan ini, Anda perlu mengganti titik asal koordinat (0; 0) ke dalam pertidaksamaan ini. Jika koordinat titik asal memenuhi pertidaksamaan, maka penyelesaian pertidaksamaan tersebut adalah setengah bidang tempat titik asal koordinat berada. Jika koordinatnya tidak memenuhi pertidaksamaan, maka penyelesaian pertidaksamaan tersebut adalah setengah bidang yang tidak memuat titik asal. Setengah bidang penyelesaian pertidaksamaan akan dilambangkan dengan guratan dari garis lurus ke setengah bidang, seperti pada Gambar 1.

Jika kita menyelesaikan sistem pertidaksamaan linier, maka setiap langkah dilakukan untuk setiap ketidaksetaraan sistem.

Contoh 1. Selesaikan ketimpangan

Larutan. Mari kita menggambar garis lurus

Substitusikan garis lurus ke dalam persamaan, kita peroleh, dan substitusikan, kita peroleh. Oleh karena itu, koordinat titik potong dengan sumbunya adalah A(3; 0) , B(0; 2) . Mari kita menggambar garis lurus melalui titik-titik ini (sekali lagi, Gambar 1).

Mari kita pilih setengah bidang solusi pertidaksamaan tersebut. Untuk melakukan ini, kita substitusikan koordinat titik asal (0; 0) ke dalam pertidaksamaan:

kita memperoleh , yaitu koordinat titik asal memenuhi pertidaksamaan ini. Oleh karena itu, penyelesaian pertidaksamaan tersebut adalah setengah bidang yang memuat titik asal koordinat, yaitu setengah bidang kiri (alias bawah).

Jika ketimpangan ini ketat, maka akan ada bentuknya

maka titik-titik pada garis batas tersebut tidak dapat menjadi penyelesaian karena tidak memenuhi pertidaksamaan.

Sekarang perhatikan sistem pertidaksamaan linier dengan dua hal yang tidak diketahui:

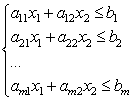
Masing-masing pertidaksamaan sistem pada bidang ini mendefinisikan setengah bidang. Suatu sistem pertidaksamaan linier disebut konsisten jika mempunyai paling sedikit satu solusi, dan tidak konsisten jika tidak mempunyai solusi. Penyelesaian sistem pertidaksamaan linier adalah setiap pasangan bilangan () yang memenuhi semua pertidaksamaan sistem tersebut.

Secara geometris, penyelesaian sistem pertidaksamaan linier adalah himpunan titik-titik yang memenuhi semua pertidaksamaan sistem, yaitu bagian persekutuan dari setengah bidang yang dihasilkan. Oleh karena itu, secara geometris, dalam kasus umum, penyelesaiannya dapat digambarkan dalam bentuk poligon, dalam kasus tertentu dapat berupa garis, segmen, atau bahkan titik. Jika suatu sistem pertidaksamaan linier tidak konsisten, maka tidak ada satu titik pun pada bidang tersebut yang memenuhi semua pertidaksamaan sistem tersebut.

Contoh 2.

Larutan. Jadi, kita perlu menemukan poligon solusi terhadap sistem pertidaksamaan ini. Mari kita buat garis batas pertidaksamaan pertama, yaitu garis, dan garis batas pertidaksamaan kedua, yaitu garis.

Kita melakukannya selangkah demi selangkah, seperti yang ditunjukkan pada referensi teoritis dan pada contoh 1, terutama karena pada contoh 1 kita membuat garis batas pertidaksamaan, yang merupakan garis pertama dalam sistem ini.

Setengah bidang solusi yang berhubungan dengan pertidaksamaan sistem ini diarsir ke dalam pada Gambar 2. Bagian umum dari setengah bidang solusi adalah sudut terbuka ABC. Artinya himpunan titik-titik pada bidang yang membentuk sudut terbuka ABC, adalah solusi untuk pertidaksamaan pertama dan kedua dari sistem, yaitu solusi untuk sistem dua pertidaksamaan linier. Dengan kata lain, koordinat titik mana pun dari himpunan ini memenuhi kedua pertidaksamaan sistem.

Contoh 3. Memecahkan sistem pertidaksamaan linier

Larutan. Mari kita buat garis batas yang sesuai dengan pertidaksamaan sistem. Kami melakukan ini dengan mengikuti langkah-langkah yang diberikan dalam bantuan teoritis untuk setiap ketidaksetaraan. Sekarang kita menentukan setengah bidang solusi untuk setiap pertidaksamaan (Gambar 3).

Setengah bidang penyelesaian yang berhubungan dengan pertidaksamaan suatu sistem diarsir ke dalam. Perpotongan setengah bidang penyelesaian digambarkan, seperti ditunjukkan pada gambar, dalam bentuk segi empat ABCE. Kami menemukan bahwa poligon solusi sistem pertidaksamaan linier dengan dua variabel adalah segiempat ABCE .

Segala sesuatu yang dijelaskan di atas tentang sistem pertidaksamaan linier dengan dua hal yang tidak diketahui juga berlaku untuk sistem pertidaksamaan dengan sejumlah hal yang tidak diketahui, dengan satu-satunya perbedaan bahwa penyelesaian pertidaksamaan dengan N yang tidak diketahui akan menjadi totalitas N bilangan () yang memenuhi semua pertidaksamaan, dan sebagai pengganti garis batas akan ada bidang hiper batas N ruang -dimensi. Solusinya adalah solusi polihedron (simplex) yang dibatasi oleh hyperplanes.

Dalam artikel ini kami akan mempertimbangkannya menyelesaikan kesenjangan. Kami akan memberi tahu Anda dengan jelas tentangnya bagaimana membangun solusi terhadap kesenjangan, disertai contoh yang jelas!

Sebelum kita membahas penyelesaian pertidaksamaan menggunakan contoh, mari kita pahami konsep dasarnya.

Informasi umum tentang kesenjangan

Ketidaksamaan adalah ekspresi yang fungsinya dihubungkan dengan tanda relasi >, . Ketimpangan dapat bersifat numerik dan literal.
Pertidaksamaan yang memiliki dua tanda perbandingan disebut ganda, dengan tiga tanda perbandingan tiga kali lipat, dan seterusnya. Misalnya:
Sebuah(x) > b(x),
a(x) a(x) b(x),
Sebuah(x) b(x).
a(x) Pertidaksamaan yang mengandung tanda > atau atau - tidak tegas.
Memecahkan ketimpangan adalah nilai variabel apa pun yang pertidaksamaannya benar.
"Selesaikan ketimpangan" artinya kita perlu menemukan himpunan semua solusinya. Ada yang berbeda metode untuk mengatasi kesenjangan. Untuk solusi ketimpangan Mereka menggunakan garis bilangan yang tak terhingga. Misalnya, solusi atas ketimpangan x > 3 adalah interval dari 3 sampai +, dan angka 3 tidak termasuk dalam interval tersebut, oleh karena itu titik pada garis tersebut dilambangkan dengan lingkaran kosong, karena ketimpangan sangat ketat.
+
Jawabannya adalah: x (3; +).
Nilai x=3 tidak termasuk dalam himpunan solusi, sehingga tanda kurungnya bulat. Tanda tak terhingga selalu diberi tanda kurung. Tanda itu berarti "milik".
Mari kita lihat cara menyelesaikan pertidaksamaan menggunakan contoh lain yang bertanda:
x 2
-+
Nilai x=2 termasuk dalam himpunan solusi, sehingga tanda kurung siku berbentuk persegi dan titik pada garis ditandai dengan lingkaran terisi.
Jawabannya adalah: x " title="Rendered oleh QuickLaTeX.com">!}

Untuk menyelesaikan suatu sistem, Anda memerlukan setiap pertidaksamaan penyusunnya. Hanya keputusan yang diambil untuk tidak menulis secara terpisah, tetapi bersama-sama, menggabungkannya dengan kurung kurawal.

Dalam setiap pertidaksamaan sistem, kita memindahkan yang tidak diketahui ke satu sisi, yang diketahui ke sisi lain dengan tanda yang berlawanan:

Judul="Diberikan oleh QuickLaTeX.com">!}

Setelah disederhanakan, kedua ruas pertidaksamaan harus dibagi dengan angka di depan X. Kami membagi pertidaksamaan pertama dengan nomor positif, jadi tanda pertidaksamaan tidak berubah. Pertidaksamaan kedua kita bagi dengan angka negatif, sehingga tanda pertidaksamaan harus dibalik:

Judul="Diberikan oleh QuickLaTeX.com">!}

Kami menandai solusi pertidaksamaan pada garis bilangan:

Sebagai tanggapan, kita tuliskan perpotongan solusinya, yaitu bagian yang terdapat bayangan pada kedua garis.

Jawaban: x∈[-2;1).

Pada pertidaksamaan pertama, kita hilangkan pecahannya. Caranya, kita mengalikan kedua ruas suku demi suku dengan penyebut terkecil 2. Jika dikalikan dengan bilangan positif, tanda pertidaksamaan tidak berubah.

Pada pertidaksamaan kedua kita membuka tanda kurung. Hasil kali jumlah dan selisih dua ekspresi sama dengan selisih kuadrat ekspresi tersebut. Di sisi kanan adalah kuadrat selisih kedua ekspresi.

Judul="Diberikan oleh QuickLaTeX.com">!}

Kami memindahkan yang tidak diketahui ke satu sisi, yang diketahui ke sisi lain dengan tanda berlawanan dan menyederhanakan:

Kita membagi kedua ruas pertidaksamaan dengan angka di depan X. Pada pertidaksamaan pertama kita bagi dengan bilangan negatif sehingga tanda pertidaksamaannya terbalik. Yang kedua kita bagi dengan bilangan positif, tanda pertidaksamaannya tidak berubah:

Judul="Diberikan oleh QuickLaTeX.com">!}

Kedua pertidaksamaan tersebut memiliki tanda “kurang dari” (tidak masalah jika salah satu tanda benar-benar “kurang dari”, tanda lainnya longgar, “kurang dari atau sama dengan”). Kita tidak dapat menandai kedua solusi tersebut, namun menggunakan aturan “ “. Semakin kecil adalah 1, maka sistem tersebut tereduksi menjadi ketimpangan

Kami menandai solusinya pada garis bilangan:

Jawaban: x∈(-∞;1).

Membuka tanda kurung. Pada pertidaksamaan pertama - . Ini sama dengan jumlah pangkat tiga dari ekspresi ini.

Yang kedua, hasil kali jumlah dan selisih dua ekspresi, yang sama dengan selisih kuadrat. Karena di sini ada tanda minus di depan tanda kurung, sebaiknya dibuka dalam dua tahap: pertama gunakan rumus, baru kemudian buka tanda kurung, ubah tanda tiap suku menjadi kebalikannya.

Kami memindahkan yang tidak diketahui ke satu arah, yang diketahui ke arah lain dengan tanda berlawanan:

Judul="Diberikan oleh QuickLaTeX.com">!}

Keduanya lebih besar dari sekedar tanda. Dengan menggunakan aturan “lebih dari lebih”, kita mereduksi sistem ketimpangan menjadi satu ketimpangan. Jadi, bilangan terbesar kedua bilangan tersebut adalah 5.

Judul="Diberikan oleh QuickLaTeX.com">!}

Kami menandai solusi pertidaksamaan pada garis bilangan dan menuliskan jawabannya:

Jawaban: x∈(5;∞).

Karena dalam sistem aljabar pertidaksamaan linier terjadi tidak hanya sebagai masalah independen, tetapi juga dalam penyelesaiannya berbagai jenis persamaan, pertidaksamaan, dll., penting untuk menguasai topik ini tepat waktu.

Lain kali kita akan melihat contoh penyelesaian sistem pertidaksamaan linier dalam kasus khusus ketika salah satu pertidaksamaan tidak memiliki solusi atau solusinya berupa bilangan apa pun.